题目内容
20.先化简$\frac{{x}^{2}-9}{{x}^{2}-6x+9}$,然后在不等式5-2x>-1整数解中选一个使原式有意义的数代入求值.分析 将分子、分母因式分解后约分即可化简分式,再解不等式得出x的整数值,代入求值可得.
解答 解:$\frac{{x}^{2}-9}{{x}^{2}-6x+9}$=$\frac{(x+3)(x-3)}{(x-3)^{2}}$=$\frac{x+3}{x-3}$,
∵5-2x>-1,
∴-2x>-6,
∴x<3,
则不等式的整数解中取x=2,
∴原式=$\frac{2+3}{2-3}$=-5.
点评 本题主要考查分式的化简求值及解不等式的能力,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.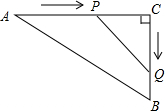 如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
 如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )| A. | 5秒 | B. | 20秒 | C. | 5秒或20秒 | D. | 不确定 |
15.若平面内有点A、B、C,过其中任意两点画直线,则最多可以画的条数是( )
| A. | 3条 | B. | 4条 | C. | 5条 | D. | 6条 |
12.如图所示的立体图形中,含有曲面的是( )


| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (2)(4) |
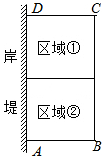 为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为a米(a为大于21的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过21米.设AB的长为x米,矩形区域ABCD的面积为y平方米
为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为a米(a为大于21的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过21米.设AB的长为x米,矩形区域ABCD的面积为y平方米