题目内容
8. 已知二次函数y=-x2+2x+m.
已知二次函数y=-x2+2x+m.(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
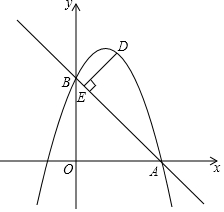
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,求直线AB与这个二次函数的解析式;
(3)在直线AB上方的抛物线上有一动点D,当D与直线AB的距离DE最大时,求点D的坐标,并求DE最大距离是多少?
分析 (1)根据抛物线与x轴有两个交点时,△>0,即可得到结论;
(2)把点A(3,0)代入y=-x2+2x+m得到-9+6+m=0得到B(0,3),
解方程组即可得到结论;
(3)过点D作y轴的垂线,垂足为C,再过点A作AG⊥CD,垂足为G,连接BD,AD,得到当DE的值越大时,S△ADB的面积越大,设D(x,y),DC=x,BC=y-3,DG=3-x,AG=y根据图形的面积公式即可得到结论.
解答 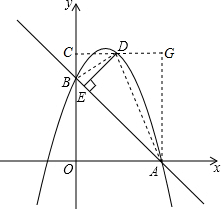 解:(1)当抛物线与x轴有两个交点时,△>0,即4+4m>0,
解:(1)当抛物线与x轴有两个交点时,△>0,即4+4m>0,
∴m>-1;
(2)∵点A(3,0)在抛物线y=-x2+2x+m上,
∴-9+6+m=0,∴m=3.
∴抛物线解析式为y=-x2+2x+3,且B(0,3),
设直线AB的解析式为y=kx+b,将A(3,0),B(0,3)代入y=kx+b中,得到
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线AB的解析式为y=-x+3;
(3)过点D作y轴的垂线,垂足为C,再过点A作AG⊥CD,垂足为G,连接BD,AD,
∵AB为定值,∴当DE的值越大时,S△ADB的面积越大,
设D(x,y),DC=x,BC=y-3,DG=3-x,AG=y
∴S△ADB=S梯形AGCB-S△BDC-S△ADG,
∴S△ADB=$\frac{3(y-3+y)}{2}$-$\frac{1}{2}$(y-3)x-$\frac{1}{2}$(3-x)y=-$\frac{3}{2}$(x-$\frac{3}{2}$)2+$\frac{27}{8}$,
∵a=-$\frac{3}{2}$<0,
∴当$x=\frac{3}{2}$时,S△ADB的最大值=$\frac{27}{8}$,
将$x=\frac{3}{2}$代入y=-x2+2x+3,得到$y=\frac{15}{4}$,即D($\frac{3}{2}$,$\frac{15}{4}$),
又∵S△ADB=$\frac{1}{2}$DE•AB,且AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=3$\sqrt{2}$,
∴$\frac{1}{2}$×3$\sqrt{2}$DE=$\frac{27}{8}$.
∴DE=$\frac{9\sqrt{2}}{8}$,
答:DE的最大值为$\frac{9\sqrt{2}}{8}$.
点评 本题主要考查了待定系数法求二次函数和一次函数的解析式,抛物线上点的坐标特征,勾股定理,确定当DE的值越大时,S△ADB的面积越大是解题的关键.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案| A. | 5.2×10-8 | B. | 52×10-9 | C. | 0.52×10-7 | D. | 5.2×10-7 |
| A. | 1cm 2cm 4cm | B. | 8cm 6cm 4cm | C. | 12cm 5cm 6cm | D. | 2cm 3cm 6cm |
| A. | 有且只有一条直线垂直于已知直线 | |
| B. | 从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 | |
| C. | 直线b外一点A与直线b上各点连接而成的所有线段中,最短线段的长是5cm,则点A到直线b的距离是5cm | |
| D. | 同旁内角互补 |
| A. | $\sqrt{27}$ | B. | $\sqrt{1\frac{1}{3}}$ | C. | -$\sqrt{75}$ | D. | $\sqrt{18}$ |
 甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.根据图象信息,填空
甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.根据图象信息,填空