题目内容
 如图,在△ABC中,∠C=60°,AB=14,AC=10,求BC的长.
如图,在△ABC中,∠C=60°,AB=14,AC=10,求BC的长.考点:勾股定理
专题:
分析:过A点作AD垂直BC于D点.因为BC=CD+BD,可先由∠C=60°,AD⊥BC,AC=10,求得AD的长,进而在△ADB中根据勾股定理可求得BD的长.即可求BC的长.
解答:解:如图过A点作AD⊥BC于D点.
在Rt△ABD中,AC=10,∠C=60°,
∴CD=
AC=5,AD=5
,
∵AB=14,
∴BD=
=11,
∴BC=CD+BD=16.

在Rt△ABD中,AC=10,∠C=60°,
∴CD=
| 1 |
| 2 |
| 3 |
∵AB=14,
∴BD=
| AB2-AD2 |
∴BC=CD+BD=16.
点评:此题考查了解直角三角形,涉及的知识点:三角函数和勾股定理.解题的关键是过A点作AD垂直BC于D点,构成直角三角形.

练习册系列答案
相关题目
 如图所示,在长为5cm,宽为3cm的长方形内部有一平行四边形,则平行四边形的面积为( )
如图所示,在长为5cm,宽为3cm的长方形内部有一平行四边形,则平行四边形的面积为( )| A、7cm2 |
| B、8cm2 |
| C、9cm2 |
| D、10cm2 |
 如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB.BE与CF有怎样的位置关系?为什么?
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB.BE与CF有怎样的位置关系?为什么?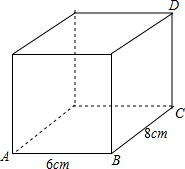 如图所示,一个长方体的纸盒,它的长、宽分别是6cm,8cm,最长能放一根长26cm的木棒,这个纸盒的高应是多少?说明你的理由.
如图所示,一个长方体的纸盒,它的长、宽分别是6cm,8cm,最长能放一根长26cm的木棒,这个纸盒的高应是多少?说明你的理由.