题目内容
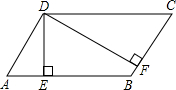 如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,DE:DF=2:3,?ABCD的周长是50,求?ABCD各边的长.
如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,DE:DF=2:3,?ABCD的周长是50,求?ABCD各边的长.考点:平行四边形的性质
专题:
分析:根据平行四边形的性质可得AD=BC,DC=AB,再根据周长是50可得AB+BC=25,根据平行四边形的面积可得AB•DE=BC•DF,由DE:DF=2:3可得AB:BC=3:2,进而可得答案.
解答:解:∵四边形ABCD是平行四边形,
∴AD=BC,DC=AB,
∵?ABCD的周长是50,
∴AB+BC=25,
∵S平行四边形ABCD=AB•DE=BC•DF,
∵DE:DF=2:3,
∴AB:BC=3:2,
∴AB=25×
=15,CB=25×
=10.
∴CD=15,AD=10.
∴AD=BC,DC=AB,
∵?ABCD的周长是50,
∴AB+BC=25,
∵S平行四边形ABCD=AB•DE=BC•DF,
∵DE:DF=2:3,
∴AB:BC=3:2,
∴AB=25×
| 3 |
| 5 |
| 2 |
| 5 |
∴CD=15,AD=10.
点评:此题主要考查了平行四边形的性质和面积,关键是掌握平行四边形的对边相等.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
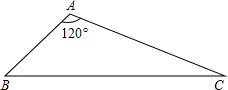 如图,AB=2,AC=4,∠BAC=120°,求BC及S△ABC.
如图,AB=2,AC=4,∠BAC=120°,求BC及S△ABC. 如图,在△ABC中,中位线EF与中线AD相交于点O.求证:AD与EF互相平分.
如图,在△ABC中,中位线EF与中线AD相交于点O.求证:AD与EF互相平分.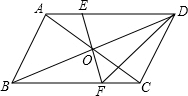 如图,AC、BD为?ABCD的对角线,O为两条对角线的交点,过点O作EF⊥BD,与AD、BC分别交于点E、F,试猜想DE与DF之间的关系,并说明理由.
如图,AC、BD为?ABCD的对角线,O为两条对角线的交点,过点O作EF⊥BD,与AD、BC分别交于点E、F,试猜想DE与DF之间的关系,并说明理由.
 如图所示的组合体,请画出它的三视图.
如图所示的组合体,请画出它的三视图. 如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.
如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由. 如图,已知:OE、OF分别是AB、AC的垂直平分线,∠OBC、∠OCB的平分线交于点P,求证:OP⊥BC.
如图,已知:OE、OF分别是AB、AC的垂直平分线,∠OBC、∠OCB的平分线交于点P,求证:OP⊥BC. 有一块三角形的草地,它的一条边长为25m,在图纸上,这条边的长为5cm,其他两条边的长都为4cm,求其他两边的实际长度.
有一块三角形的草地,它的一条边长为25m,在图纸上,这条边的长为5cm,其他两条边的长都为4cm,求其他两边的实际长度.