题目内容
12.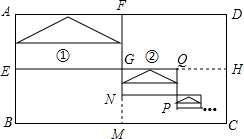 如图,在矩形ABCD中,AD=4,AB=2,连接其对边中点,得到四个矩形,顺次连接AF、FG、AE三边的中点,得到三角形①;连接矩形GMCH对边的中点,又得到四个矩形,顺次连接GQ、QP、GN三边的中点,得到三角形②;…;如此操作下去,得到三角形
如图,在矩形ABCD中,AD=4,AB=2,连接其对边中点,得到四个矩形,顺次连接AF、FG、AE三边的中点,得到三角形①;连接矩形GMCH对边的中点,又得到四个矩形,顺次连接GQ、QP、GN三边的中点,得到三角形②;…;如此操作下去,得到三角形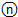 ,则三角形
,则三角形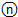 的面积为$\frac{1}{{2}^{2n-1}}$.
的面积为$\frac{1}{{2}^{2n-1}}$.
分析 根据矩形的性质和三角形的面积公式求出三角形①、②、③的面积,得出规律写出第n个三角形的面积.
解答 解:∵矩形ABCD的长AD=4,宽AB=2,
∴AF=2,AE=1,
则S三角形①=$\frac{1}{2}$×2×$\frac{1}{2}$=$\frac{1}{2}$;
S三角形②=$\frac{1}{2}$×1×$\frac{1}{4}$=$\frac{1}{{2}^{3}}$;
S三角形③=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{8}$=$\frac{1}{{2}^{5}}$;
…
∴S三角形n=$\frac{1}{{2}^{2n-1}}$,
故答案为:$\frac{1}{{2}^{2n-1}}$.
点评 本题考查的是矩形的性质,掌握三角形的面积公式、通过计算找出规律是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图,a∥b,AB⊥a,BC交于b于E,若∠1=47°,则∠2的度数是( )
如图,a∥b,AB⊥a,BC交于b于E,若∠1=47°,则∠2的度数是( )
 如图,a∥b,AB⊥a,BC交于b于E,若∠1=47°,则∠2的度数是( )
如图,a∥b,AB⊥a,BC交于b于E,若∠1=47°,则∠2的度数是( )| A. | 137° | B. | 133° | C. | 120° | D. | 100° |
20. 把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
 把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )
把两块三角板按如图所示拼在一起,∠BOC=58°,则∠AOD的大小是( )| A. | 90° | B. | 100° | C. | 120° | D. | 122° |
7.如果$\sqrt{3a+12}$是二次根式,那么a的取值范围是( )
| A. | a≥-4 | B. | a≤-4 | C. | a≠-4 | D. | a>4 |
17.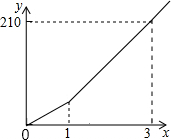 一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
 一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )| A. | 70千米/时 | B. | 75千米/时 | C. | 105千米/时 | D. | 210千米/时 |

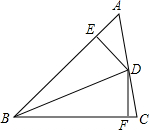 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.
如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.