题目内容
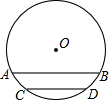 如图,AB、CD都是⊙O的弦,且AB∥CD.求证:AC=BD.
如图,AB、CD都是⊙O的弦,且AB∥CD.求证:AC=BD.考点:圆心角、弧、弦的关系,全等三角形的判定与性质
专题:证明题
分析:连接OA、OC、OD、OB,如图,根据等腰三角形的性质,由OC=OD得∠C=∠D,再利用平行线的性质得∠1=∠C,∠2=∠D,则∠1=∠2,接着利用三角形外角性质得∠1=∠A+∠3,∠2=∠B+∠4,加上∠A=∠B,则∠3=∠4,根据圆心角、弧、弦的关系得到
=
,于是有AC=BD.
 |
| AC |
 |
| BD |
解答: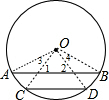 证明:连接OA、OC、OD、OB,如图,
证明:连接OA、OC、OD、OB,如图,
∵OC=OD,
∴∠C=∠D,
∵AB∥CD,
∴∠1=∠C,∠2=∠D,
∴∠1=∠2,
∵OA=OB,
∴∠A=∠B,
而∠1=∠A+∠3,∠2=∠B+∠4,
∴∠3=∠4,
∴
=
,
∴AC=BD.
 证明:连接OA、OC、OD、OB,如图,
证明:连接OA、OC、OD、OB,如图,∵OC=OD,
∴∠C=∠D,
∵AB∥CD,
∴∠1=∠C,∠2=∠D,
∴∠1=∠2,
∵OA=OB,
∴∠A=∠B,
而∠1=∠A+∠3,∠2=∠B+∠4,
∴∠3=∠4,
∴
 |
| AC |
 |
| BD |
∴AC=BD.
点评:本题考查了圆心角、弧、弦的关系:同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等;推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
 如图所示,在Rt△ABC中,∠BAC=90°,点D,E在BC上,且BE=AB,CD=AC,求∠DAE的度数.
如图所示,在Rt△ABC中,∠BAC=90°,点D,E在BC上,且BE=AB,CD=AC,求∠DAE的度数. 如图,AB、CD相交于点O,且∠C=∠B,若AC=4cm,AO=3cm,BD=8cm.
如图,AB、CD相交于点O,且∠C=∠B,若AC=4cm,AO=3cm,BD=8cm. 已知△ABC中,∠C=90°,∠A=40°,CD是AB边上的高,CE是∠BCA的角平分线,分别交AB于点D、E.求∠ECD的度数.
已知△ABC中,∠C=90°,∠A=40°,CD是AB边上的高,CE是∠BCA的角平分线,分别交AB于点D、E.求∠ECD的度数.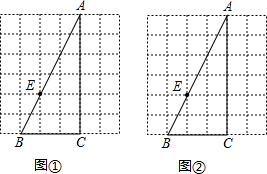 如图,已知△ABC中,∠C=90°,点E在边AB上,请过点E作一条直线,与△ABC的其他边相交于一点D,使得以点A、E、D为顶点的三角形与△ABC相似,并求它们的周长之比.
如图,已知△ABC中,∠C=90°,点E在边AB上,请过点E作一条直线,与△ABC的其他边相交于一点D,使得以点A、E、D为顶点的三角形与△ABC相似,并求它们的周长之比. 如图所示,一座抛物线型拱桥,拱顶O离水面高4米,水面宽度AB=10米,现有一竹排运送一只货箱欲从桥下经过,已知货箱长10米,宽6米,高2.4米(竹排与水面持平),问货箱能否顺利通过该桥?
如图所示,一座抛物线型拱桥,拱顶O离水面高4米,水面宽度AB=10米,现有一竹排运送一只货箱欲从桥下经过,已知货箱长10米,宽6米,高2.4米(竹排与水面持平),问货箱能否顺利通过该桥? 如图,直线AB、CD、EF相交于O点,已知∠AOE=20°,∠DOB=52°,OG平分∠COF.求∠EOG的度数.
如图,直线AB、CD、EF相交于O点,已知∠AOE=20°,∠DOB=52°,OG平分∠COF.求∠EOG的度数.