题目内容
11.解方程组(1)$\left\{\begin{array}{l}x=3y\\ x+4y=14\end{array}\right.$
(2)$\left\{\begin{array}{l}{y-1=3(x-2)}\\{y+4=2(x+1)}\end{array}\right.$.
分析 (1)应用代入法,求出二元一次方程组的解是多少即可.
(2)应用加减消元法,求出二元一次方程组的解是多少即可.
解答 解:(1)$\left\{\begin{array}{l}{x=3y(1)}\\{x+4y=14(2)}\end{array}\right.$
(1)代入(2),可得3y+4y=14,
解得y=2,
把y=2代入(1),可得x=6,
∴方程组的解为:$\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{y-1=3(x-2)(1)}\\{y+4=2(x+1)(2)}\end{array}\right.$
(1)-(2),可得x-8=-5,
解得x=3,
把x=3代入(1),可得y=4,
∴方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$.
点评 此题主要考查了二元一次方程组的解法,要熟练掌握,注意代入法、加减消元法的应用.

练习册系列答案
相关题目
1.函数y=$\frac{x+2}{x-5}$中自变量x的取值范围是( )
| A. | x>5 | B. | x<5 | C. | x≠5 | D. | x=5 |
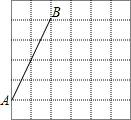 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上. 如图,已知抛物线y=ax2+bx(a≠0)经过A(-2,0),B(-3,3),顶点为C.
如图,已知抛物线y=ax2+bx(a≠0)经过A(-2,0),B(-3,3),顶点为C. 如图,直线y=-x-1与双曲线$y=\frac{-2}{x}$交于A、B两点.
如图,直线y=-x-1与双曲线$y=\frac{-2}{x}$交于A、B两点.