题目内容
1.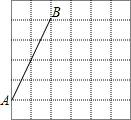 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.(1)在方格纸中画出以AB为一边的等腰△ABC,点C在小正方形的顶点上,且△ABC的面积为6.
(2)在方格纸中画出△ABC的中线BD,并将△BCD向右平移1个单位长度得到△EFG(点B、C、D的对应点分别为E、F、G),画出△EFG,并直接写出△BCD和△EFG重叠部分图形的面积.
分析 (1)利用等腰三角形的性质结合三角形面积求法得出答案;
(2)利用平移的性质得出对应点位置,再利用相似三角形的性质得出S△MNG=$\frac{1}{4}$S△BCD,进而得出答案.
解答  解:(1)如图所示:△ABC,即为所求;
解:(1)如图所示:△ABC,即为所求;
(2)如图所示:△EFG,即为所求,
△BCD和△EFG重叠部分图形的面积为:$\frac{1}{4}$×$\frac{1}{2}$×2×3=$\frac{3}{4}$.
点评 此题主要考查了平移变换以及三角形面积求法等知识,根据题意正确把握平移的性质是解题关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
9.下列调查中,适合用全面调查方式的是( )
| A. | 了解我国东海水域是否受到日本核辐射污染 | |
| B. | 了解我们班50名同学上次月考数学成绩 | |
| C. | 了解一批节能灯泡的使用寿命 | |
| D. | 了解一批我国最新生产的核弹头的杀伤半径 |
6.下面的函数是反比例函数的是( )
| A. | y=3x+l | B. | y=x2+2x | C. | y=$\frac{2}{x}$ | D. | y=$\frac{x}{2}$ |