题目内容
17.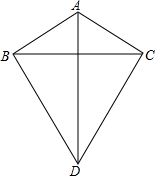 如图所示,四边形ABDC中,AD同时平分∠BAC和∠BDC,问:B,C两点是否关于直线AD对称?请证明.
如图所示,四边形ABDC中,AD同时平分∠BAC和∠BDC,问:B,C两点是否关于直线AD对称?请证明.
分析 根据全等三角形的判定和性质得出AB=AC,BD=CD,根据线段垂直平分线的判定得到点A,点D在BC的垂直平分线上,于是得到直线AD是线段BC的对称轴,进而判断B,C两点关于直线AD对称即可.
解答 解:B,C两点关于直线AD对称,
理由:∵AD同时平分∠BAC和∠BDC,
∴∠BAD=∠CAD,∠BDA=∠CDA,
在△ABD与△ACD中,
$\left\{\begin{array}{l}{∠BAD=∠CAD}\\{AD=AD}\\{∠BDA=∠CDA}\end{array}\right.$,
∴△ABD≌△ACD,
∴AB=AC,BD=CD,
∴点A,点D在BC的垂直平分线上,
∴AD垂直平分BC,
∴直线AD是线段BC的对称轴,
∴B,C两点是关于直线AD对称.
点评 本题考查了全等三角形的判定和性质,轴对称的性质,线段垂直平分线的性质,熟练掌握各性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.学业考试体育测试结束后,某班体育委员将本班50名学生的测试成绩制成如下的统计表.这个班学生体育测试成绩的众数是( )
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 1 | 2 | 4 | 5 | 6 | 5 | 8 | 10 | 6 | 2 |
| A. | 30分 | B. | 28分 | C. | 25分 | D. | 10人 |
2.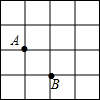 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )| A. | $\frac{6}{25}$ | B. | $\frac{1}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{7}{25}$ |

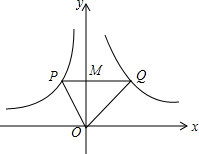 如图,点P(-1,2)、Q(2,2)分别位于两个不同的双曲线上,则S△POQ=3.
如图,点P(-1,2)、Q(2,2)分别位于两个不同的双曲线上,则S△POQ=3.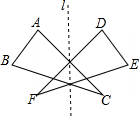 如图,△ABC沿着直线l翻折,与△DEF完全重合,那么我们就说这两个三角形成轴对称.请判断下列说法是否正确.并更正错误的.
如图,△ABC沿着直线l翻折,与△DEF完全重合,那么我们就说这两个三角形成轴对称.请判断下列说法是否正确.并更正错误的.