Question

如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．

（1）求直线BD和抛物线的解析式．

（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．

（3）在抛物线上是否存在点P，使S_△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．

Answer 1

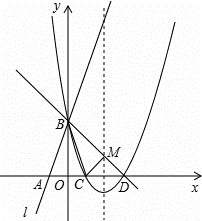
解：（1）直线BD的解析式为：y=-x+3．

            抛物线的解析式为：y=x²﹣4x+3．   

（2）抛物线的解析式为：y=x²﹣4x+3=（x﹣2）²﹣1，

∴抛物线的对称轴为直线x=2，顶点坐标为（2，﹣1）．直线BD：y=﹣x+3与抛物线的对称轴交于点M，令x=2，得y=1，∴M（2，1）．设对称轴与x轴交点为点F，则CF=FD=MN=1，

∴△MCD为等腰直角三角形．∵以点N、B、D为顶点的三角形与△MCD相似，

∴△BND为等腰直角三角形．

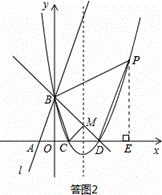（I）若BD为斜边，则易知此时直角顶点为原点O，∴N₁（0，0）；

（II）若BD为直角边，B为直角顶点，则点N在x轴负半轴上，

∵OB=OD=ON₂=3，∴N₂（﹣3，0）；

（III）若BD为直角边，D为直角顶点，则点N在y轴负半轴上，

∵OB=OD=ON₃=3，∴N₃（0，﹣3）．

∴满足条件的点N坐标为：（0，0），（﹣3，0）或（0，﹣3）．

（3）假设存在点P，使S_△PBD=6，设点P坐标为（m，n）．

（I）当点P位于直线BD上方时，如答图2所示：

过点P作PE⊥x轴于点E，则PE=n，DE=m﹣3．

S_△PBD=S_梯形PEOB﹣S_△BOD﹣S_△PDE=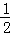（3+n）•m﹣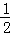×3×3﹣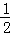（m﹣3）•n=6，

化简得：m+n=7 ①，

∵P（m，n）在抛物线上，

∴n=m²﹣4m+3，代入①式整理得：m²﹣3m﹣4=0，

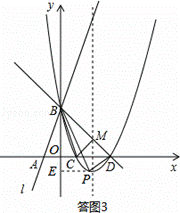解得：m₁=4，m₂=﹣1，∴n₁=3，n₂=8，

∴P₁（4，3），P₂（﹣1，8）；

（II）当点P位于直线BD下方时，如答图3所示：

过点P作PE⊥y轴于点E，则PE=m，OE=﹣n，BE=3﹣n．

S_△PBD=S_梯形PEOD+S_△BOD﹣S_△PBE=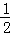（3+m）•（﹣n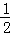）+×3×3﹣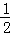（3﹣n）•m=6，

化简得：m+n=﹣1 ②，∵P（m，n）在抛物线上，∴n=m²﹣4m+3，

代入②式整理得：m²﹣3m+4=0，△=﹣7＜0，此方程无解．

故此时点P不存在．

综上,在抛物线上存在点P，使S_△PBD=6，点P的坐标为（4，3）或（﹣1，8）．