题目内容
13.已知关于x的二次函数y=mx2-(3m-1)x+2m-2的图象与x轴的两交点的距离为2,且开口向上.(1)求此抛物线的解析式;
(2)当直线y=x+b与(1)中的图象只有两个交点时,求b的取值范围.
分析 (1)设抛物线与x轴两交点的横坐标为x1,x2,则两交点之间距离为|x1-x2|=2,再与根与系数关系的等式结合变形,可求m的值,从而确定抛物线的解析式;
(2)根据图象有两个交点,可得判别式大于零,根据解不等式,可得答案.
解答 解:(1)设x1,x2为抛物线y=mx2-(3m-1)x+2m-2与x轴交点的横坐标,
则有x1+x2=$\frac{3m-1}{m}$,x1•x2=$\frac{2m-2}{m}$
由|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(\frac{3m-1}{m})^{2}-\frac{4(2m-2)}{m}}$=$\sqrt{\frac{(m+1)^{2}}{{m}^{2}}}$=|$\frac{m+1}{m}$|,
由|x1-x2|=2,且开口向上,得
$\frac{m+1}{m}$=2,
∴m=1
∴所求抛物线的解析式为:y1=x2-2x;
(2)联立抛物线与直线,得
$\left\{\begin{array}{l}{y={x}^{2}-2x}\\{y=x+b}\end{array}\right.$,
消元,得
x2-3x-b=0,△=9+4b>0,
解得b>-$\frac{9}{4}$,
当b>-$\frac{9}{4}$时,直线y=x+b与(1)中的图象只有两个交点.
点评 本题考查了抛物线与x轴得交点,具有较强的综合性,利用了一元二次方程的根的情况,二次函数与对应的一元二次方程的联系.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
6.-$\frac{1}{4}$的相反数与绝对值等于$\frac{1}{4}$的数的和应等于( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$或0 |
2.关于等边三角形,下列说法中错误的是( )
| A. | 等边三角形中,各边都相等 | |
| B. | 等边三角形是特殊的等腰三角形 | |
| C. | 三个角都等于60°的三角形是等边三角形 | |
| D. | 有一个角为60°的等腰三角形不是等边三角形 |
5.下列命题错误的是( )
| A. | 经过不在同一直线上的三个点一定可以作圆 | |
| B. | 三角形的外心到三角形各顶点的距离相等 | |
| C. | 经过切点且垂直于切线的直线必经过圆心 | |
| D. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 |
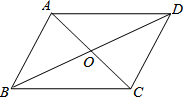 如图,?ABCD的周长是28cm,△ABC的周长是22cm,对角线交于点O,则OC的长为4cm.
如图,?ABCD的周长是28cm,△ABC的周长是22cm,对角线交于点O,则OC的长为4cm. 如图,在△ABC中,AB=AC,点D在AC上,且在AB的垂直平分线上.若∠A=40°,则∠DBC=30°.
如图,在△ABC中,AB=AC,点D在AC上,且在AB的垂直平分线上.若∠A=40°,则∠DBC=30°.