题目内容
20.已知关于x的方式方程$\frac{x-3}{x-2}$=2-$\frac{m}{2-x}$会产生增根,则m=-1.分析 分式方程去分母转化为整式方程,由分式方程有增根,得到x-2=0,求出x的值,代入整式方程求出m的值即可.
解答 解:去分母得:x-3=2x-4+m,
由分式方程有增根,得到x-2=0,即x=2,
把x=2代入整式方程得:m=-1,
故答案为:-1.
点评 此题考查了分式方程的增根,增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.

练习册系列答案
相关题目
10. 如图,下列条件中,能使平行四边形ABCD成为矩形的是( )
如图,下列条件中,能使平行四边形ABCD成为矩形的是( )
 如图,下列条件中,能使平行四边形ABCD成为矩形的是( )
如图,下列条件中,能使平行四边形ABCD成为矩形的是( )| A. | AB=BC | B. | AB=CD | C. | AC⊥BD | D. | AC=BD |
15.下列多项式中,能用公式法分解因式的是( )
| A. | -m2+n2 | B. | a2-2ab-b2 | C. | m2+n2 | D. | -a2-b2 |
5.下列等式成立的是( )
| A. | $\frac{0.1a}{0.1a-b}$=$\frac{a}{a-b}$ | B. | $\frac{-a}{a-b}$=$\frac{a}{a+b}$ | C. | $\frac{a}{a+b}$=$\frac{1}{b}$ | D. | $\frac{a}{b}$=$\frac{ab}{{b}^{2}}$ |
12.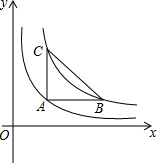 已知b>a>0,如图,过函数y=$\frac{a}{x}$(x>0)图象上一点A作AB平行于x轴,交函数y=$\frac{b}{x}$(x>0)的图象于点B,过点A作AC平行于y轴,交函数y=$\frac{b}{x}$(x>0)的图象于点C,则△ABC的面积为( )
已知b>a>0,如图,过函数y=$\frac{a}{x}$(x>0)图象上一点A作AB平行于x轴,交函数y=$\frac{b}{x}$(x>0)的图象于点B,过点A作AC平行于y轴,交函数y=$\frac{b}{x}$(x>0)的图象于点C,则△ABC的面积为( )
 已知b>a>0,如图,过函数y=$\frac{a}{x}$(x>0)图象上一点A作AB平行于x轴,交函数y=$\frac{b}{x}$(x>0)的图象于点B,过点A作AC平行于y轴,交函数y=$\frac{b}{x}$(x>0)的图象于点C,则△ABC的面积为( )
已知b>a>0,如图,过函数y=$\frac{a}{x}$(x>0)图象上一点A作AB平行于x轴,交函数y=$\frac{b}{x}$(x>0)的图象于点B,过点A作AC平行于y轴,交函数y=$\frac{b}{x}$(x>0)的图象于点C,则△ABC的面积为( )| A. | $\frac{a-b}{2}$ | B. | $\frac{(a-b)^{2}}{2}$ | C. | $\frac{(a-b)^{2}}{2a}$ | D. | $\frac{(a-b)^{2}}{2b}$ |
10.下列计算正确的是( )
| A. | x3•x2=x5 | B. | x5÷x=x3 | C. | (x2)3=x5 | D. | (3x)2=6x2 |
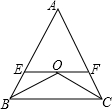 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,EF∥BC,EF经过点O,若AB=10,AC=15,则△AEF的周长是( )
如图,△ABC中,BO平分∠ABC,CO平分∠ACB,EF∥BC,EF经过点O,若AB=10,AC=15,则△AEF的周长是( ) 如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),求证:BE=DE.
如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),求证:BE=DE.