题目内容
我们知道:选用同一长度单位量得两条线段AB、CD的长度分别是m,n,那么就说两条线段的比AB:CD=m:
n,如果把
表示成比值k,那么
=k,或AB=kCD.请完成以下问题:
(1)四条线段a,b,c,d中,如果 ,那么这四条线段a,b,c,d叫做成比例线段.
(2)已知
=
=2,那么
= ,
=
(3)如果
=
,那么
=
成立吗?请用两种方法说明其中的理由.
(4)如果
=
=
=m,求m的值.
n,如果把
| m |
| n |
| AB |
| CD |
(1)四条线段a,b,c,d中,如果
(2)已知
| a |
| b |
| c |
| d |
| a+b |
| b |
| c+d |
| d |
(3)如果
| a |
| b |
| c |
| d |
| a-b |
| b |
| c-d |
| d |
(4)如果
| x+y |
| z |
| y+z |
| x |
| z+x |
| y |
考点:比例线段
专题:
分析:(1)根据成比例线段的定义作答;
(2)由
=
=2,得a=2b,c=2d,代入计算即可求解;
(3)利用等式的性质两边减去1即可证明;设
=
=k,那么a=kb,c=kd,代入即可证明;
(4)可分x+y+z=0和x+y+z≠0两种情况代入求值和利用等比性质求解.
(2)由
| a |
| b |
| c |
| d |
(3)利用等式的性质两边减去1即可证明;设
| a |
| b |
| c |
| d |
(4)可分x+y+z=0和x+y+z≠0两种情况代入求值和利用等比性质求解.
解答:解:(1)四条线段a,b,c,d中,如果a:b=c:d,那么这四条线段a,b,c,d叫做成比例线段;
(2)∵
=
=2,
∴a=2b,c=2d,
∴
=
=3,
=
=3.
(3)如果
=
,那么
=
成立.理由如下:
证明一:∵
=
,
∴
-1=
-1,即
-
=
-
,
∴
=
;
证明二:设
=
=k,那么a=kb,c=kd,
∵
=
=k-1,
=
=k-1,
∴
=
;
(4)①当x+y+z=0时,
y+z=-x,z+x=y,x+y=-z,
∴m为其中任何一个比值,即m=
=-1;
②x+y+z≠0时,
m=
=
=2.
所以m=2或-1.
故答案为a:b=c:d;3,3.
(2)∵
| a |
| b |
| c |
| d |
∴a=2b,c=2d,
∴
| a+b |
| b |
| 2b+b |
| b |
| c+d |
| d |
| 2d+d |
| d |
(3)如果
| a |
| b |
| c |
| d |
| a-b |
| b |
| c-d |
| d |
证明一:∵
| a |
| b |
| c |
| d |
∴
| a |
| b |
| c |
| d |
| a |
| b |
| b |
| b |
| c |
| d |
| d |
| d |
∴
| a-b |
| b |
| c-d |
| d |
证明二:设
| a |
| b |
| c |
| d |
∵
| a-b |
| b |
| kb-b |
| b |
| c-d |
| d |
| kd-d |
| d |
∴
| a-b |
| b |
| c-d |
| d |
(4)①当x+y+z=0时,
y+z=-x,z+x=y,x+y=-z,
∴m为其中任何一个比值,即m=
| -x |
| x |
②x+y+z≠0时,
m=
| y+z+z+x+x+y |
| x+y+z |
| 2(x+y+z) |
| x+y+z |
所以m=2或-1.
故答案为a:b=c:d;3,3.
点评:本题考查了比例线段的定义:对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就说这四条线段是成比例线段,简称比例线段.同时考查了比例的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若分式方程
=
有增根,则增根x等于( )
| x2 |
| x-1 |
| 1 |
| x-1 |
| A、1 | B、-1 | C、0 | D、±1 |
 如图,DE⊥AB于E,∠A=25°,∠D=45°,求∠ACB的度数.
如图,DE⊥AB于E,∠A=25°,∠D=45°,求∠ACB的度数.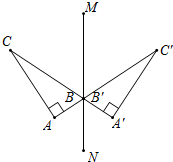 如图,Rt△ABC关于直线MN的对称点分别为A′、B′、C′,其中∠A=90°,AC=8cm,A′C=12cm.
如图,Rt△ABC关于直线MN的对称点分别为A′、B′、C′,其中∠A=90°,AC=8cm,A′C=12cm. 如图,这四幅图是一个正方体不同的侧面,六个面上分别写着A、B、C、D、E、F,则C、A、E的对面字母分别是
如图,这四幅图是一个正方体不同的侧面,六个面上分别写着A、B、C、D、E、F,则C、A、E的对面字母分别是


