题目内容
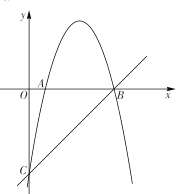
【题目】如图,抛物线![]() 与直线
与直线![]() 交于
交于![]() 两点,交
两点,交![]() 轴与
轴与![]() 两点,连接
两点,连接![]() 已知
已知![]() .
.
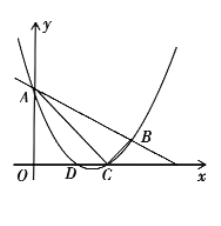
(1)求抛物线的解析式;
(2)求证:![]() 是直角三角形;
是直角三角形;
(3)![]() 为
为![]() 轴右侧抛物线上一动点,连接
轴右侧抛物线上一动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,问:是否存在点
,问:是否存在点![]() 使得以
使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)存在,满足条件的点
;(2)见解析;(3)存在,满足条件的点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() .
.
【解析】
(1)将点A,C的坐标代入到抛物线的解析式中,即可求出答案;
(2)先将抛物线解析式与直线解析式联立求出B点坐标,然后利用勾股定理求出![]() ,然后利用勾股定理的逆定理即可得出结论;
,然后利用勾股定理的逆定理即可得出结论;
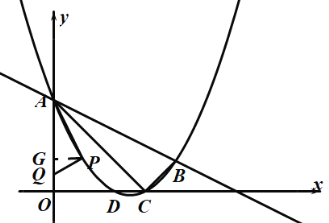
(3)过点![]() 作
作![]() 轴于
轴于![]() 则
则![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,分四种情况:①若点
,分四种情况:①若点![]() 在点
在点![]() 的下方,当
的下方,当![]() 时;②若点
时;②若点![]() 在点
在点![]() 的下方,当
的下方,当![]() 时;③若点
时;③若点![]() 在点
在点![]() 的上方,当
的上方,当![]() 时;④若点
时;④若点![]() 在点
在点![]() 的上方,当
的上方,当![]() 时,分别进行计算即可.
时,分别进行计算即可.
(1)把![]() 代入
代入![]()
得: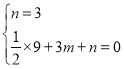 ,解得:
,解得: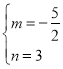 ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
(2)由题意联立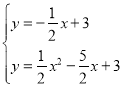 ,
,
解得:![]() 或
或![]() ,
,
![]() B点的坐标为
B点的坐标为![]() ,
,
![]()
![]() ,
,
![]() 是直角三角形;
是直角三角形;
(3)存在点![]() 使得以
使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
过点![]() 作
作![]() 轴于
轴于![]() 则
则![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,由
,由![]() 在
在![]() 轴右侧可得
轴右侧可得![]() 则
则![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
①若点![]() 在点
在点![]() 的下方,当
的下方,当![]() 时,则
时,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,则
,则![]() .
.
把![]() 代入
代入![]() ,
,
得![]() ,
,
整理得:![]() ,
,
解得:![]() (舍去),
(舍去),![]() (舍去);
(舍去);
②若点![]() 在点
在点![]() 的下方,当
的下方,当![]() 时,则
时,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,则
,则![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,
,
整理得:![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
![]() ;
;
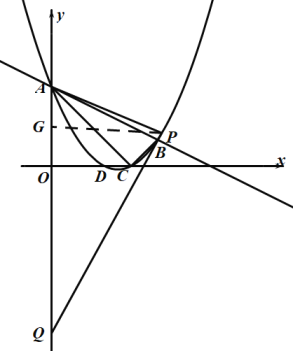
③若点![]() 在点
在点![]() 的上方,当
的上方,当![]() 时,则
时,则![]() ,
,
同理可得:点![]() 的坐标为
的坐标为![]() ;
;
④若点![]() 在点
在点![]() 的上方,当
的上方,当![]() 时,则
时,则![]() ,
,
同理可得:点![]() 的坐标为
的坐标为![]() ;
;
综上所述:满足条件的点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() .
.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?