题目内容
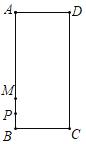
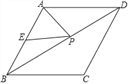
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上的动点(不与
上的动点(不与![]() 重合).过
重合).过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .设
.设![]() 的长度为
的长度为![]() ,
,![]() 与
与![]() 的长度和为
的长度和为![]() .则能表示
.则能表示![]() 与
与![]() 之间的函数关系的图象大致是( )
之间的函数关系的图象大致是( )
A.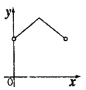 B.
B.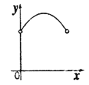 C.
C.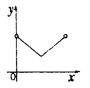 D.
D.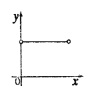
【答案】D
【解析】
根据三角形面积得出S△PAB=![]() PEAB;S△PAB=S△PQB+S△PAQ=
PEAB;S△PAB=S△PQB+S△PAQ=![]() QNPB+
QNPB+![]() PAMQ,进而得出y=
PAMQ,进而得出y=![]() ,即可得出答案.
,即可得出答案.
解:连接PQ,作PE⊥AB垂足为E,
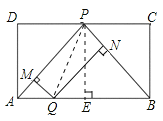
∵过Q作QM⊥PA于M,QN⊥PB于N,
∴S△PAB=![]() PEAB;
PEAB;
S△PAB=S△PQB+S△PAQ=![]() QNPB+
QNPB+![]() PAMQ,
PAMQ,
∵矩形ABCD中,P为CD中点,
∴PA=PB,
∵QM与QN的长度和为y,
∴S△PAB=S△PQB+S△PAQ=![]() QNPB+
QNPB+![]() PAMQ=
PAMQ=![]() PB(QM+QN)=
PB(QM+QN)=![]() PBy,
PBy,
∴S△PAB=![]() PEAB=
PEAB=![]() PBy,
PBy,
∴y=![]() ,
,
∵PE=AD,
∴PE,AB,PB都为定值,
∴y的值为定值,符合要求的图形为D,
故选:D.

练习册系列答案
相关题目
【题目】某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:
价格/类型 | A型 | B型 |
进价(元/只) | 15 | 35 |
标价(元/只) | 25 | 50 |
(1)这两种文具盒各购进多少只?
(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?