Question

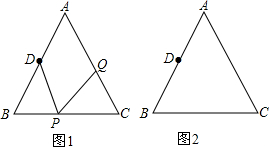
17．如图，已知△ABC中，AB=AC=8厘米，BC=6厘米，∠B=∠C，点D为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
（1）若点Q的运动速度与点P的运动速度相同，是否会出现某一时刻△BPD与△CPQ全等的情况？为什么？（若不能全等，说明理由；若能够全等，求出这个时刻）
（2）若点Q的运动速度与点P的运动速度不相同，是否会出现某一时刻△BPD与△CPQ全等的情况？为什么？（若不能全等，说明理由；若能够全等，求出这个时刻以及Q点的坐标）

Answer 1

分析 （1）根据两边及夹角分别相等的两个三角形全等，可得PC与BD的关系，根据解方程，可得答案；
（2）根据两边及夹角分别相等的两个三角形全等，可得PC与BP的关系，CQ与BD的关系，根据解方程，可得答案．

解答 解：（1）点Q的运动速度与点P的运动速度相同，会出现某一时刻△BPD与△CPD全等的情况，
则CQ=BP=3t，PC=6-3t，
PC=BD=4，
即6-3t=4
解得t=$\frac{2}{3}$，
当t=$\frac{2}{3}$时，△BPD与△CQP全等；
（2）设Q点的速度为a，运动t秒时两三角形全等，
BP=3t，CP=6-3t，BD=4，CQ=at，
所以当CP=BP，CQ=BD时，三角形全等，
即6-3t=3t，
解得t=1，
因为at=4，a=4，
当t=1，a=4cm/s时，△BPD与△CPQ全等．

点评 本体考察了全等三角形的判定，利用了两边及夹角分别相等的两个三角形全等得出关于t的方程是解题关键．