题目内容
12.已知:一次函数y=$\frac{\sqrt{3}}{3}$x+m与反比例函数y=$\frac{\sqrt{3}}{x}$的图象在第一象限的交点为A(1,n).(1)求m与n的值;
(2)设一次函数的图象与x轴交于点B,C为x轴上一点,连接AC,若△ABC为等腰三角形,求C的坐标.
分析 (1)把点A(1,n)代入反比例函数y=$\frac{\sqrt{3}}{x}$的解析式即可求出n,再把点A坐标代入y=$\frac{\sqrt{3}}{3}$x+m即可求出m.
(2)分三种情形讨论①点B为等腰三角形的顶角的顶点.②点C为等腰三角形的顶角的顶点.③点A为等腰三角形的顶角的顶点.求出点C坐标即可.
解答 解:(1)∵A(1,n)在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,
∴n=$\sqrt{3}$,
∵一次函数y=$\frac{\sqrt{3}}{3}$x+m经过点A(1,$\sqrt{3}$),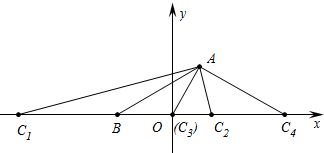
∴$\sqrt{3}$=$\frac{\sqrt{3}}{3}$+m,
∴m=$\frac{2\sqrt{3}}{3}$.
(2)∵一次函数y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交x轴于B,
∴点B(-2,0),
∴AB=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,OA=2,
如图所示,当BC=BA时,点C的坐标为C1(-2-2$\sqrt{3}$,0),C2(2$\sqrt{3}$-2,0),
当CB=CA时,点C与原点重合,点C坐标(0,0),
当AB=AC时,点C的坐标C4(4,0)
综上所述满足条件的点C坐标(-2-2$\sqrt{3}$,0)或(2$\sqrt{3}$-2,0)或(0,0)或(4,0).
点评 本题考查反比例函数的图象与一次函数图象的交点问题,解题的关键是灵活正确待定系数法,学会分类讨论的思想,注意考虑问题要全面,属于中考常考题型.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | $\sqrt{a}$+$\sqrt{b}$=$\sqrt{ab}$ | B. | (-a2)2=-a4 | C. | (a-2)2=a2-4 | D. | $\sqrt{a}$÷$\sqrt{b}$=$\sqrt{\frac{a}{b}}$(a≥0,b>0) |
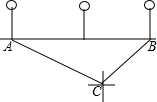 周末,小明一家去东昌湖划船,当船划到湖中C点处时,湖边的路灯A位于点C的北偏西64°方向上,路灯B位于点C的北偏东44°方向上,已知每两个路灯之间的距离是50米,求此时小明一家离岸边的距离是多少米?(精确到1米)(参考数据:
周末,小明一家去东昌湖划船,当船划到湖中C点处时,湖边的路灯A位于点C的北偏西64°方向上,路灯B位于点C的北偏东44°方向上,已知每两个路灯之间的距离是50米,求此时小明一家离岸边的距离是多少米?(精确到1米)(参考数据:

 在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于2.
在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于2.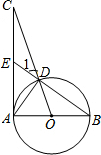 如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.