题目内容
1.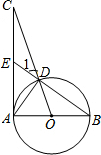 如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
分析 (1)由AB为⊙O的直径,AC为⊙O的切线,易证得∠CAD=∠BDO,继而证得结论;
(2)由(1)易证得△CAD∽△CDE,然后由相似三角形的对应边成比例,求得CD的长,再利用勾股定理,求得答案.
解答 (1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
∵AC为⊙O的切线,
∴OA⊥AC,
∴∠OAD+∠CAD=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠1=∠BDO,
∴∠1=∠CAD;
(2)解:∵∠1=∠CAD,∠C=∠C,
∴△CAD∽△CDE,
∴CD:CA=CE:CD,
∴CD2=CA•CE,
∵AE=EC=2,
∴AC=AE+EC=4,
∴CD=2$\sqrt{2}$,
设⊙O的半径为x,则OA=OD=x,
则Rt△AOC中,OA2+AC2=OC2,
∴x2+42=(2$\sqrt{2}$+x)2,
解得:x=$\sqrt{2}$.
∴⊙O的半径为$\sqrt{2}$.
点评 此题考查了切线的性质、圆周角定理以及相似三角形的判定与性质.注意证得△CAD∽△CDE是解此题的关键.

练习册系列答案
相关题目
9.今年百色市九年级参加中考人数约有38900人,数据38900用科学记数法表示为( )
| A. | 3.89×102 | B. | 389×102 | C. | 3.89×104 | D. | 3.89×105 |
11.为鼓励居民节约用水,某市决定对居民用水收费实行“阶梯价”,即当每月用水量不超过15吨时,采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费.小兰家四、五月份的用水量及收费情况如下表:
(1)求该市每吨水的基本价和市场价.
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式.
(3)小兰家6月份的用水量为26吨,则她家要缴水费多少元?
(4)若小兰家7月份的水费为165元,则她家7月份用水多少吨?
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式.
(3)小兰家6月份的用水量为26吨,则她家要缴水费多少元?
(4)若小兰家7月份的水费为165元,则她家7月份用水多少吨?
9.下列方程组中,以$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$为解的二元一次方程组是( )
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=3}\\{x-y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=-1}\\{x-y=-3}\end{array}\right.$ |
 某几何体的三视图如图所示,则组成该几何体的小正方体的个数是5.
某几何体的三视图如图所示,则组成该几何体的小正方体的个数是5.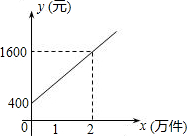 某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题: