题目内容
20．化简求值：$\frac{a}{{a}^{2}-4}$•$\frac{a+2}{{a}^{2}-3a}$-$\frac{1}{2-a}$，其中a=$\sqrt{2}$+3．分析 原式第一项约分后，两项通分并利用同分母分式的加法法则计算，约分得到最简结果，把a的值代入计算即可求出值．
解答 解：原式=$\frac{a}{（a+2）（a-2）}$•$\frac{a+2}{a（a-3）}$+$\frac{1}{a-2}$=$\frac{1}{（a-2）（a-3）}$+$\frac{a-3}{（a-2）（a-3）}$=$\frac{a-2}{（a-2）（a-3）}$=$\frac{1}{a-3}$，
当a=$\sqrt{2}$+3时，原式=$\frac{\sqrt{2}}{2}$．
点评 此题考查了分式的化简运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
15．比$\sqrt{5}$大的数是（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | 2 | D． | $\frac{5}{2}$ |
5．不改变分式的值，使分式$\frac{{\frac{1}{2}{x^2}+\frac{1}{3}}}{{\frac{1}{2}{x^2}-\frac{1}{3}{x^3}}}$的分子和分母各项的系数是整数，化简的结果为（ ）
| A． | $\frac{{2{x^2}+3}}{{2{x^2}-3{x^3}}}$ | B． | $\frac{{3{x^2}+2}}{{2{x^2}-3{x^3}}}$ | C． | $\frac{{3{x^2}+2}}{{3{x^2}-2{x^3}}}$ | D． | $\frac{{3{x^2}+2}}{{3{x^3}-2{x^2}}}$ |
9．今年百色市九年级参加中考人数约有38900人，数据38900用科学记数法表示为（ ）
| A． | 3.89×102 | B． | 389×102 | C． | 3.89×104 | D． | 3.89×105 |
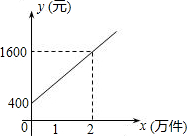某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系，其图象如图所示．根据图象提供的信息，解答下列问题：