题目内容
7.若点P(m,n)在直角坐标系的第二象限,则一次函数y=mx+n的大致图象是( )| A. | 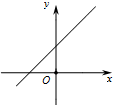 | B. |  | C. | 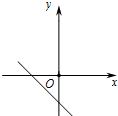 | D. | 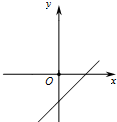 |
分析 利用第二象限点的坐标特征得到m<0,n>0,然后根据一次函数图象与系数的关系可判断一次函数y=mx+n经过的象限,从而可对各选项进行判断.
解答 解:∵点P(m,n)在直角坐标系的第二象限,
∴m<0,n>0,
∴一次函数y=mx+n经过第一、二、四象限.
故选B.
点评 本题考查了一次函数的图象:一次函数y=kx+b的图象为直线.解决此题的主要方法是利用一次函数图象与系数的关系确定直线的大致位置.

练习册系列答案
相关题目
15.比$\sqrt{5}$大的数是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{5}{2}$ |
2.在平面直角坐标系中点P(-2,3)和Q(m,n)关于x轴对称,则m的值为( )
| A. | m=-2 | B. | m=2 | C. | m=-3 | D. | m=3 |
19.某校要从甲、乙、丙、丁四名学生中选一名参加“汉字听写”大赛,选拔中每名学生的平均成绩$\overline{x}$及其方差s2如表所示,如果要选拔一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8.9 | 9.5 | 9.5 | 8.9 |
| s2 | 0.92 | 0.92 | 1.01 | 1.03 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
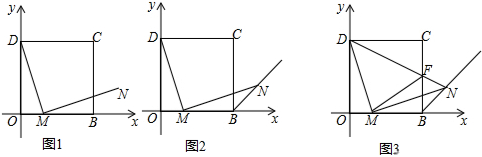
 某几何体的三视图如图所示,则组成该几何体的小正方体的个数是5.
某几何体的三视图如图所示,则组成该几何体的小正方体的个数是5.