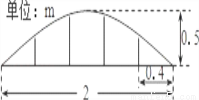
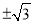��Ŀ����
����������һ���ڽǦ�����һ���ڽǦµ�����ʱ�����dzƴ�������Ϊ�����������Ρ������Ц���Ϊ�������ǡ������һ�������������Ρ��ġ������ǡ�Ϊ100�㣬��ô��������������Ρ�����С�ڽǵĶ���Ϊ________��
30�� �����������������������Ҫ�������¶����Լ������ε��ڽǺͶ�����������֪�ó��µĶ����ǽ���ؼ���������֪һ���ڽǦ�����һ���ڽǦµ������ó��µĶ��������������С�ڽǼ��ɣ� ������ã���=2�£���=110�㣬���=55�㣬 180��-110��-55��=15�㣬 �ʴ�Ϊ��15�㣮
��ϰ��ϵ�д�
 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
�����Ŀ



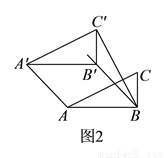
 ����ͼ
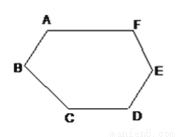
����ͼ ���ı���
���ı��� �У�
�У� 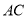 ƽ��
ƽ��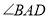 ��
�� 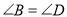 ����֤���ı���
����֤���ı���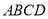 Ϊ���ڱ��ı��Σ�
Ϊ���ڱ��ı��Σ�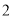 ����ͼ
����ͼ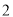 ��
�� 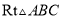 ��
�� 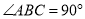 ��
�� 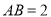 ��
�� 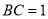 ����
����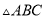 ��
��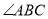 ��ƽ����
��ƽ����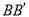 �ķ���ƽ�ƣ��õ�
�ķ���ƽ�ƣ��õ�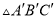 ������
������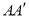 ��
��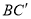 ����ƽ�ƺ���ı���
����ƽ�ƺ���ı���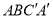 �ǵ��ڱ��ı��Σ���ƽ�Ƶľ��룮
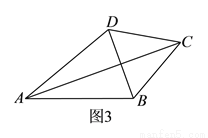
�ǵ��ڱ��ı��Σ���ƽ�Ƶľ��룮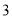 ����ͼ
����ͼ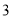 ���ڵ��ڱ��ı���
���ڵ��ڱ��ı���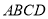 �У�
�� 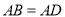 ��
�� 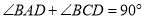 ��
�� 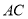 ��
��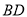 Ϊ�ı��ζԽ��ߣ�
Ϊ�ı��ζԽ��ߣ� 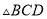 Ϊ�ȱ������Σ���̽��
Ϊ�ȱ������Σ���̽��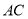 ��
��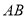 ��������ϵ��
��������ϵ��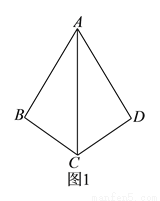
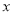 �ķ�ʽ����
�ķ�ʽ����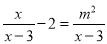 ����������
����������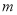 ��ֵΪ�� ����
��ֵΪ�� ����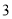 B.
B. 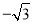 C.
C. 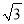 D.
D.