题目内容
12.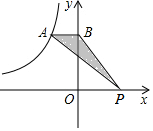 如图所示,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为4,则这个反比例函数的解析式为y=-$\frac{8}{x}$.
如图所示,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为4,则这个反比例函数的解析式为y=-$\frac{8}{x}$.
分析 连接OA,设反比例函数的解析式为y=$\frac{k}{x}$(k≠0),根据△ABO和△ABP同底等高,利用反比例函数系数k的几何意义结合△ABP的面积为4即可求出k值,再根据反比例函数在第二象限有图象,由此即可确定k值,此题得解.
解答 解:连接OA,如图所示.
设反比例函数的解析式为y=$\frac{k}{x}$(k≠0).
∵AB⊥y轴,点P在x轴上,
∴△ABO和△ABP同底等高,
∴S△ABO=S△ABP=$\frac{1}{2}$|k|=4,
解得:k=±8.
∵反比例函数在第二象限有图象,
∴k=-8,
∴反比例函数的解析式为y=-$\frac{8}{x}$.
故答案为:y=-$\frac{8}{x}$.
点评 本题考查了反比例函数系数k的几何意义以及反比例函数图象,根据反比例函数系数k的几何意义找出$\frac{1}{2}$|k|=4是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.下列运算正确的是( )
| A. | (-2a3)2=-4a6 | B. | (a+b)2=a2+b2 | C. | a2•a3=a6 | D. | a3+2a3=3a3 |
3.运用乘法公式计算(m-2)2的结果是( )
| A. | m2-4 | B. | m2-2m+4 | C. | m2-4m+4 | D. | m2+4m-4 |
20.若点A(2,-3)、B(-3,n)在同一个反比例函数的图象上,则n的值为( )
| A. | -2 | B. | 2 | C. | -6 | D. | 6 |
7.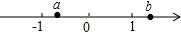 实数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
实数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
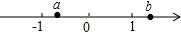 实数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
实数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )| A. | a+b<0 | B. | a-b>0 | C. | $\frac{a}{b}$<0 | D. | |a|•|b|<0 |
17.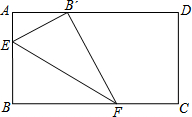 如图,在矩形ABCD中,AB=8,将矩形的一角折叠,将点B落在边AD上的B?点处,若AB=4,则折痕EF的长度为( )
如图,在矩形ABCD中,AB=8,将矩形的一角折叠,将点B落在边AD上的B?点处,若AB=4,则折痕EF的长度为( )
 如图,在矩形ABCD中,AB=8,将矩形的一角折叠,将点B落在边AD上的B?点处,若AB=4,则折痕EF的长度为( )
如图,在矩形ABCD中,AB=8,将矩形的一角折叠,将点B落在边AD上的B?点处,若AB=4,则折痕EF的长度为( )| A. | 8 | B. | 4$\sqrt{5}$ | C. | 5$\sqrt{5}$ | D. | 10 |
1.3月7日,在百度中输入“世界关注中国两会”,得到相关结果约有 2040000个,将2040000用科学记数法表示是( )
| A. | 2.04×106 | B. | 2.04×105 | C. | 2.04×104 | D. | 204×104 |
 如图,△ABC中,∠C=90°,AC=6,AB=10,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则OD的长为$\frac{4\sqrt{13}}{7}$.
如图,△ABC中,∠C=90°,AC=6,AB=10,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则OD的长为$\frac{4\sqrt{13}}{7}$.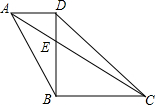 如图,在四边形ABCD中,连接AC,BD,AC和BD相交于点E.若AD∥BC,BD⊥AD,2DE=BE,$\sqrt{3}$AD=BD,则∠BAC+∠BCA的度数为60°.
如图,在四边形ABCD中,连接AC,BD,AC和BD相交于点E.若AD∥BC,BD⊥AD,2DE=BE,$\sqrt{3}$AD=BD,则∠BAC+∠BCA的度数为60°.