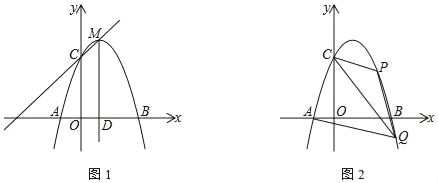题目内容
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ;
;

(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 在第四象限的抛物线上,连接
在第四象限的抛物线上,连接![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)见解析;(3)(5,
;(2)见解析;(3)(5,![]() )
)
【解析】
(1)设点A的坐标为(a,0),从而求出点B的坐标,然后代入解析式即可求出结论;
(2)先求出点A、B、C的坐标,设点R的坐标为(m,![]() ),用含m的式子表示出OE、RE,然后根据相似三角形的判定定理证出△OAD∽△ERD,△BOC∽△GEC,最后列出比例式即可求出DE和RG,从而证出结论;
),用含m的式子表示出OE、RE,然后根据相似三角形的判定定理证出△OAD∽△ERD,△BOC∽△GEC,最后列出比例式即可求出DE和RG,从而证出结论;
(3)过点N作NH⊥CE于E,作∠DFE=45°,用含m的式子表示出DE、EF、DF,设HN=n,,易知CH=n,OH=OC-CH=4-n,根据![]() 即可求出m与n的关系,然后根据锐角三角函数的性质可证∠HEN=∠FRD,再根据相似三角形的判定定理证出△RFD∽△DFG,列出比例式即可求出m的值,从而求出结论.
即可求出m与n的关系,然后根据锐角三角函数的性质可证∠HEN=∠FRD,再根据相似三角形的判定定理证出△RFD∽△DFG,列出比例式即可求出m的值,从而求出结论.
解:(1)设点A的坐标为(a,0),a<0
∵![]()
∴点B的坐标为(-2a,0)
将点A、B的坐标代入![]() 中,得
中,得

解得:![]() 或
或![]() (不符合前提条件,舍去)
(不符合前提条件,舍去)
∴抛物线的解析式为![]() ;
;
(2)由(1)得点A(-2,0),点B(4,0),点C(0,4)
设点R的坐标为(m,![]() ),其中m>0
),其中m>0
∴OA=2,OB=4,OC=4,OE=![]() ,RE=m
,RE=m
∵![]() 轴
轴
∴RE∥x轴
∴△OAD∽△ERD,△BOC∽△GEC
∴![]() ,
,![]()
即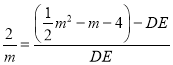 ,
,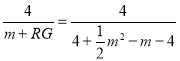
解得: DE![]() ,RG
,RG![]()
∴DE=RG;
(3)过点N作NH⊥CE于E,作∠DFE=45°
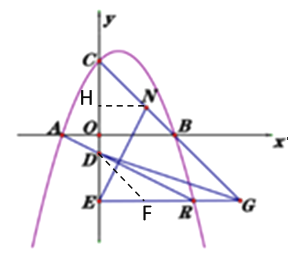
∴DE=EF=![]() ,DF=
,DF=![]() =
=![]()
设HN=n,(n>0),易知CH=n,OH=OC-CH=4-n,
由(2)知OE=![]() ,DE=RG
,DE=RG![]() ,RE= m,FR=RE-EF=
,RE= m,FR=RE-EF=![]() ,FG=FR+RG=m
,FG=FR+RG=m
∵![]()
∴EH2+HN2=EN2=DR2=DE2+RE2
∴(![]() +4-n)2+n 2 =(
+4-n)2+n 2 =(![]() )2+m2
)2+m2
解得:n=![]() 或n=m(由图可知:R的横坐标m>点B的横坐标4>n,故舍去)
或n=m(由图可知:R的横坐标m>点B的横坐标4>n,故舍去)
∴HN=![]() ,EH=m
,EH=m
∴tan∠HEN=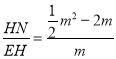 ,tan∠FRD=
,tan∠FRD=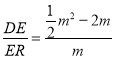
∴∠HEN=∠FRD
∵![]() ,∠DFE=45°
,∠DFE=45°
∴∠FRD+∠DGE=45°,∠DGE+∠FDG=45°
∴∠FRD=∠FDG
∵∠RFD=∠DFG
∴△RFD∽△DFG
∴![]()
即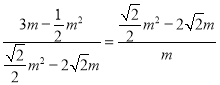
解得:m1=2,m2=5
当m=2时,点R的纵坐标为![]() =4,(点R在第四象限,故舍去)
=4,(点R在第四象限,故舍去)
当m=5时,点R的纵坐标为![]() =
=![]() ,
,
∴点R的坐标为(5,![]() )
)

【题目】某班“数学兴趣小组”对函数![]() ,的图象和性质进行了探究过程如下,请补充完成:
,的图象和性质进行了探究过程如下,请补充完成:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________________;
的取值范围是__________________;
(2)下表是![]() 与
与![]() 的几组对应值.请直接写出
的几组对应值.请直接写出![]() ,
,![]() 的值:
的值:![]() ______________;
______________;![]() ________.
________.
| … |
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| -3 | 5 | 3 |
|
| … |
(3)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
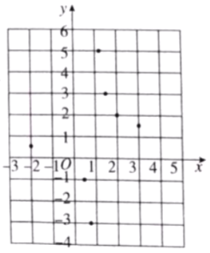
(4)通过观察函数的图象,小明发现该函数图象与反比例函数![]() 的图象形状相同,是中心对称图形,且点
的图象形状相同,是中心对称图形,且点![]() 和
和![]() 是一组对称点,则其对称中心的坐标为________.
是一组对称点,则其对称中心的坐标为________.
(5)请写出一条该函数的性质:___________________.
(6)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有实数解,求
有实数解,求![]() 的取值范围.
的取值范围.