题目内容
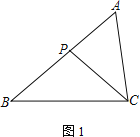
【题目】如图,直角三角形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,将
中点,将![]() 绕
绕![]() 点旋转
点旋转![]() 得到
得到![]() .一动点
.一动点![]() 从
从![]() 出发,以每秒1的速度沿
出发,以每秒1的速度沿![]() 的路线匀速运动,过点
的路线匀速运动,过点![]() 作直线
作直线![]() ,使
,使![]() .
.

(1)当点![]() 运动2秒时,另一动点
运动2秒时,另一动点![]() 也从
也从![]() 出发沿
出发沿![]() 的路线运动,且在
的路线运动,且在![]() 上以每秒1的速度匀速运动,在
上以每秒1的速度匀速运动,在![]() 上以每秒2的速度匀速运动,过
上以每秒2的速度匀速运动,过![]() 作直线
作直线![]() 使
使![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 直线
直线![]() 与
与![]() 截四边形
截四边形![]() 所得图形的面积为
所得图形的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
(2)当点![]() 开始运动的同时,另一动点
开始运动的同时,另一动点![]() 从
从![]() 处出发沿
处出发沿![]() 的路线运动,且在
的路线运动,且在![]() 上以每秒
上以每秒![]() 的速度匀速运动,在
的速度匀速运动,在![]() 上以每秒2的速度匀度运动,是否存在这样的
上以每秒2的速度匀度运动,是否存在这样的![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 运动的时间
运动的时间![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
【答案】(1)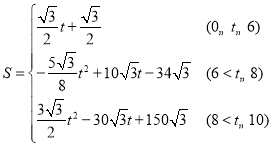 ,S的最大值为
,S的最大值为![]() ;(2)存在,m的值为
;(2)存在,m的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)分![]() 、
、![]() 和
和![]() 三种情况分别表示出有关线段求得两个变量之间的函数关系即可.
三种情况分别表示出有关线段求得两个变量之间的函数关系即可.
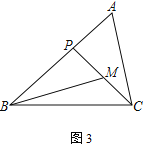
(2)分两种情形:①如图![]() 中,由题意点
中,由题意点![]() 在
在![]() 上运动的时间与点
上运动的时间与点![]() 在
在![]() 上运动的时间相等,即
上运动的时间相等,即![]() .当
.当![]() 时,当
时,当![]() 时,当
时,当![]() 时,分别构建方程求解即可.②如图
时,分别构建方程求解即可.②如图![]() 中,作
中,作![]() 于
于![]() .首先证明
.首先证明![]() ,根据
,根据![]() 构建方程即可解决问题.
构建方程即可解决问题.
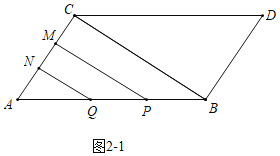
解:(1)如图![]() 中,当
中,当![]() 时,点
时,点![]() 与点
与点![]() 都在
都在![]() 上运动,
上运动,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 此时两平行线截平行四边形
此时两平行线截平行四边形![]() 的面积为
的面积为![]() .
.
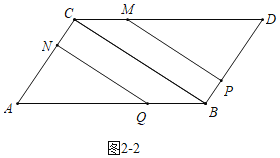
如图![]() 中,当
中,当![]() 时,点
时,点![]() 在
在![]() 上运动,点
上运动,点![]() 仍在
仍在![]() 上运动.
上运动.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
而![]() ,
,
故此时两平行线截平行四边形![]() 的面积为:
的面积为:
![]()
![]()
![]() ,
,
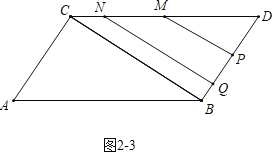
如图![]() 中,当
中,当![]() 时,点
时,点![]() 和点
和点![]() 都在
都在![]() 上运动.
上运动.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 此时两平行线截平行四边形
此时两平行线截平行四边形![]() 的面积为
的面积为![]() .
.
故![]() 关于
关于![]() 的函数关系式为
的函数关系式为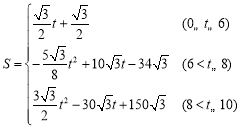 ,
,
当![]() 时,S随t增大而增大,
时,S随t增大而增大,
当![]() 时,S随t增大而增大,
时,S随t增大而增大,
当![]() 时,S随t增大而减小,
时,S随t增大而减小,
∴当t=8时,S最大,代入可得S=![]() ;
;
(2)如图![]() 中,
中,
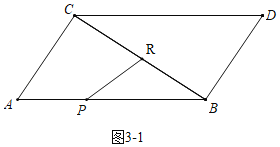
由题意点![]() 在
在![]() 上运动的时间与点
上运动的时间与点![]() 在
在![]() 上运动的时间相等,
上运动的时间相等,![]() .
.
当![]() 时,
时,![]() ,则有
,则有![]() ,解得
,解得![]() ,
,
当![]() 时,则有
时,则有![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,则有
,则有![]() ,解得
,解得![]() .
.
如图![]() 中,作
中,作![]() 于
于![]() .
.
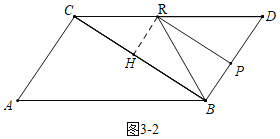
在Rt△CHR中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
当![]() 时,则有
时,则有![]() ,解得
,解得![]() ,
,
综上所述,满足条件的m的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案