题目内容
5.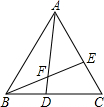 如图所示,△ABC为等边三角形,D、E分别是边BC、CA上的点,且有BD=CE,AD与BE交于点F.若AD=3,则BE的长为3.
如图所示,△ABC为等边三角形,D、E分别是边BC、CA上的点,且有BD=CE,AD与BE交于点F.若AD=3,则BE的长为3.
分析 根据等边三角形的性质证明△BCE≌△ABD(SAS)即可.
解答 解:∵△ABC为等边三角形,
∴∠ABC=∠C=60°,AB=BC,
在△BCE和△ABD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABC=∠C}\\{BD=CE}\end{array}\right.$,
∴△BCE≌△ABD(SAS),
∴AD=BE(全等三角形的对应边相等)
∵AD=3,
∴BE=3.
故答案为:3.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质.熟悉等边三角形的性质和全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
15.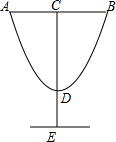 设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=( )
设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=( )
 设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=( )
设计师以y=2x2-4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=( )| A. | 17 | B. | 11 | C. | 8 | D. | 7 |
13.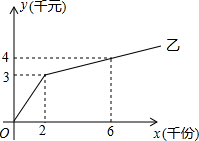 某单位准备印刷一批书面材料,现有两个印刷厂可供选择,甲厂的费用分为制作费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的费用y(千元)与书面材料数量x(千份)的关系见表:
某单位准备印刷一批书面材料,现有两个印刷厂可供选择,甲厂的费用分为制作费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的费用y(千元)与书面材料数量x(千份)的关系见表:
乙厂的印刷费用y(千元)与书面材料数量x(千份)的函数关系图象如图所示.
(1)请你写出甲厂的费用y与x的函数解析式,并在图中坐标系中画出甲厂的费用y与x的函数图象.
(2)请写出乙厂费用y与x的函数解析式,试求出当x在什么范围内时乙厂比甲厂的费用低?
(3)现有一客户需要印10千份书面材料,请问你如果是客户你如何选择?
 某单位准备印刷一批书面材料,现有两个印刷厂可供选择,甲厂的费用分为制作费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的费用y(千元)与书面材料数量x(千份)的关系见表:
某单位准备印刷一批书面材料,现有两个印刷厂可供选择,甲厂的费用分为制作费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的费用y(千元)与书面材料数量x(千份)的关系见表:| 书面材料数量x(千份) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 甲厂的印刷费用y(千元) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | … |
(1)请你写出甲厂的费用y与x的函数解析式,并在图中坐标系中画出甲厂的费用y与x的函数图象.
(2)请写出乙厂费用y与x的函数解析式,试求出当x在什么范围内时乙厂比甲厂的费用低?
(3)现有一客户需要印10千份书面材料,请问你如果是客户你如何选择?
17.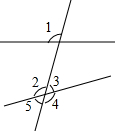 如图,下列各组角中,是对顶角的一组是( )
如图,下列各组角中,是对顶角的一组是( )
 如图,下列各组角中,是对顶角的一组是( )
如图,下列各组角中,是对顶角的一组是( )| A. | ∠1和∠2 | B. | ∠3和∠5 | C. | ∠3和∠4 | D. | ∠1和∠5 |
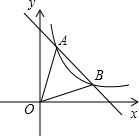 如图,一次函数y=k1x+b的图象与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点,
如图,一次函数y=k1x+b的图象与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点,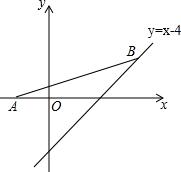 如图,点A坐标为(-2,0),点B在直线y=x-4上运动,当线段AB最短时,点B坐标为(1,-3).
如图,点A坐标为(-2,0),点B在直线y=x-4上运动,当线段AB最短时,点B坐标为(1,-3).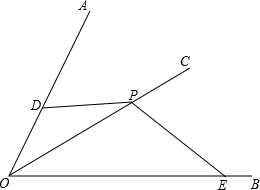 如图,OC平分∠AOB,∠DOE+∠DPE=180°.求证:PD=PE.
如图,OC平分∠AOB,∠DOE+∠DPE=180°.求证:PD=PE.