题目内容
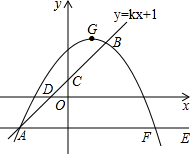 已知直线y=kx+1经过点A(d,-2)和点B(2,3),交y轴于点C,交x轴于点D.将直线AB绕点A顺时针旋转45°得到直线AE,点F(5,e)在直线AE上.经过A,B,F三点的抛物线y=ax2+bx+c的顶点为G.
已知直线y=kx+1经过点A(d,-2)和点B(2,3),交y轴于点C,交x轴于点D.将直线AB绕点A顺时针旋转45°得到直线AE,点F(5,e)在直线AE上.经过A,B,F三点的抛物线y=ax2+bx+c的顶点为G.(1)求抛物线的解析式及顶点G的坐标;
(2)将抛物线y=ax2+bx+c沿竖直方向进行平移m(m>0)个单位,顶点为G′.当∠AG′B=90°时,求m的值;
(3)在抛物线y=ax2+bx+c上是否存在点P,使△ABP的面积等于△ABG的面积的6倍?若存在,请求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)利用函数图象上点的坐标性质得出k,d的值,进而得出F点坐标,再利用待定系数法求二次函数解析式即可;
(2)分别利用①若将抛物线向上平移,②若将抛物线向下平移,分别求出M的值即可;
(3)分别求出△ABG的面积表示出△ABP的面积,进而得出等式求出即可.
(2)分别利用①若将抛物线向上平移,②若将抛物线向下平移,分别求出M的值即可;
(3)分别求出△ABG的面积表示出△ABP的面积,进而得出等式求出即可.
解答:解:(1)∵直线y=kx+1经过点A(d,-2)和点B(2,3),
∴k=1,d=-3,即直线y=x+1,A(-3,-2).
∴点C(0,1),点D(-1,0),即OC=OD.
∴∠CDO=45°.
∵直线AE是直线AB绕点A顺时针旋转45°得到的,
∴∠BAF=45°.
∴AE∥x轴.
∴点F的坐标为(5,-2).
∵抛物线y=ax2+bx+c经过A,B,F三点,
∴
解得
故抛物线的解析式为y=-
x2+
x+3=-
(x-1)2+
,故顶点G(1,
).
(2)设平移后的抛物线为y=-
(x-1)2+h,顶点G′为(1,h).
①若将抛物线向上平移.
连接AG′,BG′.作抛物线的对称轴G′H,交AE于H,则G′H⊥AE.
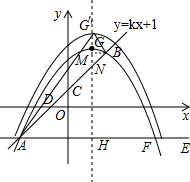
作BM⊥G′H,垂足为M.
则有AH=4,G′H=h+2,BM=1,G′M=h-3
∵∠AG′B=90°,
∴Rt△G′AH∽Rt△BG′M.
∴
=
,即
=
.
解得h=
(负号舍去).
故m=
-
=
.
②若将抛物线向下平移.
同理可得
=
,
解得h=
(正号舍去).
故m=
+
=
.
(3)设抛物线的对称轴G′H与AB的交点为N,则点N的坐标为(1,2).
∴△ABG的面积=
×(
-2)×5=
.
设点P的坐标为(p,-
p2+
p+3),
则△ABP的面积=
×(p+1+
p2-
p-3)×5=
(p2+p-6).
∵△ABP的面积等于△ABG的面积的6倍.
∴
(p2+p-6)=
×6.
解得p1=5,p2=-6,
∴-
p2+
p+3=-
×25+
×5+3=-2,
-
p2+
p+3=-
×36+
×(-6)+3=-13,
故存在点P,使△ABP的面积等于△ABG的面积的6倍,
点P的坐标为(5,-2)或(-6,-13).
∴k=1,d=-3,即直线y=x+1,A(-3,-2).
∴点C(0,1),点D(-1,0),即OC=OD.
∴∠CDO=45°.
∵直线AE是直线AB绕点A顺时针旋转45°得到的,
∴∠BAF=45°.
∴AE∥x轴.
∴点F的坐标为(5,-2).
∵抛物线y=ax2+bx+c经过A,B,F三点,
∴
|
解得
|
故抛物线的解析式为y=-
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 3 |
| 10 |
| 3 |
(2)设平移后的抛物线为y=-
| 1 |
| 3 |
①若将抛物线向上平移.
连接AG′,BG′.作抛物线的对称轴G′H,交AE于H,则G′H⊥AE.

作BM⊥G′H,垂足为M.
则有AH=4,G′H=h+2,BM=1,G′M=h-3
∵∠AG′B=90°,
∴Rt△G′AH∽Rt△BG′M.
∴
| G′H |
| BM |
| AH |
| G′M |
| h+2 |
| 1 |
| 4 |
| h-3 |
解得h=
1±
| ||
| 2 |
故m=
1+
| ||
| 2 |
| 10 |
| 3 |
3
| ||
| 6 |
②若将抛物线向下平移.
同理可得
| 3-h |
| 4 |
| 1 |
| -2-h |
解得h=
1±
| ||
| 2 |
故m=
| 10 |
| 3 |
| ||
| 2 |
3
| ||
| 6 |
(3)设抛物线的对称轴G′H与AB的交点为N,则点N的坐标为(1,2).
∴△ABG的面积=
| 1 |
| 2 |
| 10 |
| 3 |
| 10 |
| 3 |
设点P的坐标为(p,-
| 1 |
| 3 |
| 2 |
| 3 |
则△ABP的面积=
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 6 |
∵△ABP的面积等于△ABG的面积的6倍.
∴
| 5 |
| 6 |
| 10 |
| 3 |
解得p1=5,p2=-6,
∴-
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
-
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
故存在点P,使△ABP的面积等于△ABG的面积的6倍,
点P的坐标为(5,-2)或(-6,-13).
点评:此题主要考查了待定系数法求二次函数解析式以及三角形面积求法和图形的平移等知识,利用分类讨论得出是解题关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:
4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:
 某商店第一次用600元购进某种铅笔若干支,第二次又用600元购进该种铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.
某商店第一次用600元购进某种铅笔若干支,第二次又用600元购进该种铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.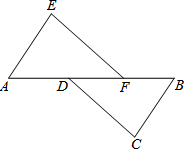 如图,A,D,F,B在同一直线上,AE=BC,且AE∥BC.添加一个条件
如图,A,D,F,B在同一直线上,AE=BC,且AE∥BC.添加一个条件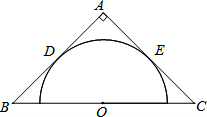 如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为
如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为 小明把如图的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是
小明把如图的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是