题目内容
某班有学生45人，会下象棋的人数是会下围棋人数的3.5倍，两种棋都会或都不会的人数都是5人，则只会下围棋的有 人．
考点：一元一次方程的应用
专题：
分析：设会下围棋的人数是x人，则会下象棋的人数为3.5x人，又因为两种棋都会及两种棋都不会的人数都是5人，则可知：会下围棋的人数+会下象棋的人数+两种棋都不会的人数-两种棋都会的人数=总人数．即可列出程求解．
解答：解：设会下围棋的人数是x人．
根据题意得：x+3.5x-5+5=45，
解得：x=10．
答；会下围棋的人数是10人．
故答案为：10．
根据题意得：x+3.5x-5+5=45，
解得：x=10．
答；会下围棋的人数是10人．
故答案为：10．
点评：考查了一元一次方程的应用，解题的关键是注意会下围棋的会下象棋的人数重复了5人，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
下列命题：
①由不在同一直线上的三条线段首尾依次相接所组成的图形叫做三角形；
②在三角形中，连接一个顶点和对边中点的直线叫做三角形的中线；
③任何三角形都有三条中线、三条内角平分线，它们都相交于一点；
④直角三角形的高只有一条．
其中正确的命题有（ ）
①由不在同一直线上的三条线段首尾依次相接所组成的图形叫做三角形；
②在三角形中，连接一个顶点和对边中点的直线叫做三角形的中线；
③任何三角形都有三条中线、三条内角平分线，它们都相交于一点；
④直角三角形的高只有一条．
其中正确的命题有（ ）
| A、一个 | B、两个 | C、三个 | D、四个 |
若单项式-
的系数为m，次数为n，则m+n=（ ）
| 3xy2 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
| D、4 |
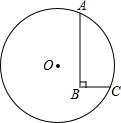如图，圆的半径是5
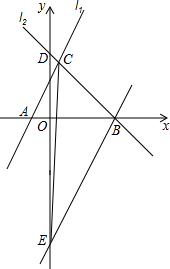如图，直线l1，l2，交于C点，直线l1与x轴交于A，直线l2与x轴交于B（3，0），与y轴交于D（0，3），已知直线l1的函数解析式为y=2x+2．