题目内容
解方程：||3x-5|+4|=8．
考点：含绝对值符号的一元一次方程
专题：
分析：根据绝对值的非负性质可得|3x-5|≥0，即可求得|3x-5|+4=8，可得3x-5=4或3x-5=-4，即可解题．
解答：解：∵|3x-5|≥0，∴|3x-5|+4＞0，
∴|3x-5|+4=8，
∴3x-5=4或3x-5=-4，
当3x-5=4时，x=3，
当3x-5=-4时，x=
，
故该方程的解为x=
或3．
∴|3x-5|+4=8，
∴3x-5=4或3x-5=-4，
当3x-5=4时，x=3，
当3x-5=-4时，x=
| 1 |
| 3 |
故该方程的解为x=
| 1 |
| 3 |
点评：本题考查了绝对值的非负性质，考查了带绝对值的一元一次方程的计算，本题中求得|3x-5|+4=8是解题的关键．
练习册系列答案
相关题目
已知函数y=（m+3）x-2，要使函数值y随自变量x的增大而减小，则m的取值范围是（ ）
| A、m≥-3 | B、m＞-3 |
| C、m≤-3 | D、m＜-3 |
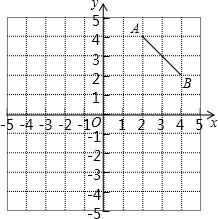如图在8×8的正方形网格中建立直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．
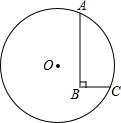如图，圆的半径是5
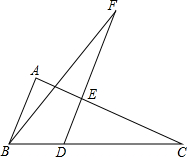如图，△ABC的面积为63，D是BC上的一点，且BD：CD=1：2，DE∥AB交AC于点E，延长DE到F，使FE：ED=2：1，连接BF，则△BDF的面积为 （ ）
如图，抛物线y=-x2+2（m+1）x+m+3与x轴交于A，B两点，且OA：OB=1：3，求m的值．