题目内容
2.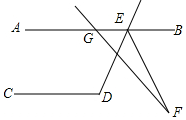 如图,AB∥CD,∠CDE=116°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F=8°.
如图,AB∥CD,∠CDE=116°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F=8°.
分析 先根据平行线的性质求出∠AED与∠DEB的度数,再由角平分线的性质求出∠DEF的度数,进而可得出∠GEF的度数,再根据三角形外角的性质即可得出结论.
解答 解:∵AB∥CD,∠CDE=116°,
∴∠AED=180°-116°=64°,∠DEB=116°.
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=$\frac{1}{2}$×116°=58°,
∴∠GEF=64°+58°=122°.
∵∠AGF=130°,
∴∠F=∠AGF-∠GEF=130°-122°=8°.
故答案为:8°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
17.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
| x | … | -2 | 0 | 1 | 2 | … |
| y | … | 7 | -1 | -2 | -1 | … |
| A. | 抛物线开口向下 | B. | 抛物线的对称轴是y轴 | ||
| C. | x<1时,y随x的增大而减小 | D. | 抛物线与y轴交于正半轴 |
14.下列各式是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{{x}^{2}+1}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{\frac{5}{3}}$ |
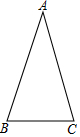 如图,在△ABC中,AB=AC,∠ABC=70°.
如图,在△ABC中,AB=AC,∠ABC=70°.