题目内容
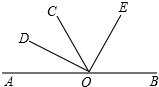 如图,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线.
如图,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线.(1)求∠DOE的度数.
(2)若只将射线OC的位置改变,其他条件不变,那么∠DOE的度数会有变化吗?
(3)若∠AOB=n°(n<180),其他条件不变,则∠DOE的度数是多少?
考点:角的计算,角平分线的定义
专题:
分析:(1)根据平角的大小和角平分线的定义即可解题;
(2)不会,∠DOE大小和射线OC无关;
(3)根据角平分线的定义即可求得∠DOE=
∠AOB.
(2)不会,∠DOE大小和射线OC无关;
(3)根据角平分线的定义即可求得∠DOE=
| 1 |
| 2 |
解答:解:(1)∵OD是∠AOC的平分线,OE是∠COB的平分线.
∴∠AOD=∠COD,∠BOE=∠COE,
∵∠AOB=180°,
∴∠DOE=∠COD+∠COE=90°;
(2)由(1)中可知,∠DOE大小和射线OC无关,
∴只将射线OC的位置改变,其他条件不变,那么∠DOE的度数不会有变化;
(3))∵OD是∠AOC的平分线,OE是∠COB的平分线.
∴∠AOD=∠COD,∠BOE=∠COE,
∵∠AOB=n,
∴∠DOE=∠COD+∠COE=
;
∴∠AOD=∠COD,∠BOE=∠COE,
∵∠AOB=180°,
∴∠DOE=∠COD+∠COE=90°;
(2)由(1)中可知,∠DOE大小和射线OC无关,
∴只将射线OC的位置改变,其他条件不变,那么∠DOE的度数不会有变化;
(3))∵OD是∠AOC的平分线,OE是∠COB的平分线.
∴∠AOD=∠COD,∠BOE=∠COE,
∵∠AOB=n,
∴∠DOE=∠COD+∠COE=
| n |
| 2 |
点评:本题考查了角的计算,考查了角平分线的定义,本题中熟练运用角平分线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知M=8x2-y2+6x-2,N=9x2+4y+13,则M-N的值( )
| A、为正数 | B、为负数 |
| C、为非正数 | D、不能确定 |
 如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,求⊙O的直径.
如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,求⊙O的直径. 已知:在△ABC中,DE∥BC,且AC2=AD•AB.求证:BD•DC=EC•CB.
已知:在△ABC中,DE∥BC,且AC2=AD•AB.求证:BD•DC=EC•CB.