Question

5．矩形ABCD的对角线AC、BD相交于点O，∠AOD=60°，AB=6$\sqrt{3}$，AE⊥BD，垂足为E，那么BD=12，BE=9．

Answer 1

分析 由矩形的性质得出∠BAD=90°，OA=OB=OC=OD=$\frac{1}{2}$BD，再证明△AOD是等边三角形，得出AD=OD=$\frac{1}{2}$BD，∠ODA=60°，由三角函数求出AD，即可得出BD，求出DE，即可得出BE．

解答 解：如图所示：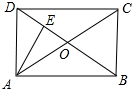
∵四边形ABCD是矩形，
∴∠BAD=90°，OA=OB=OC=OD=$\frac{1}{2}$BD，
∵∠AOD=60°，
∴△AOD是等边三角形，
∴AD=OD=$\frac{1}{2}$BD，∠ODA=60°，
∴AD=$\frac{AB}{tan60°}$=$\frac{6\sqrt{3}}{\sqrt{3}}$=6，
∴OD=6，
∴BD=2OD=12，
∵AE⊥BD，
∴DE=$\frac{1}{2}$OD=3，
∴BE=12-3=9；
故答案为：12；9．

点评 本题考查了矩形的性质、等边三角形的判定与性质、三角函数；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．