题目内容
20.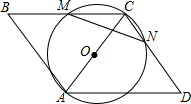 如图,在平行四边形ABCD中,以对角线AC为直径的⊙O分别交BC,CD于M,N.若AB=13,BC=14,CM=9,则MN的长度为$\frac{180}{13}$.
如图,在平行四边形ABCD中,以对角线AC为直径的⊙O分别交BC,CD于M,N.若AB=13,BC=14,CM=9,则MN的长度为$\frac{180}{13}$.
分析 连结AM,AN,根据圆周角定理可知△ABM是直角三角形,利用勾股定理即可求出AC的长;易证△AMN∽△ACD,根据相似三角形的性质即可求出MN的长.
解答 解:连结AM,AN,
∵AC是⊙O的直径,
∴∠AMC=90°,∠ANC=90°,
∵AB=13,BM=5,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=12,
∵CM=9,
∴AC=15,
∵∠MCA=∠MNA,∠MCA=∠CAD,
∴∠MNA=∠CAD,
∵∠AMN=∠ACN,
∴∠AMN=∠ACN,
∵△NMA∽△ACD,
∴AM:MN=CD:AC,
∴12:MN=13:15,
∴MN=$\frac{180}{13}$.
故答案为:$\frac{180}{13}$.
点评 本题考查了圆周角定理运用、勾股定理的运用、相似三角形的判定和性质,题目的综合性较强,难度中等,解题的关键是添加辅助线构造相似三角形.

练习册系列答案
相关题目
12.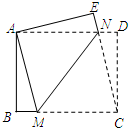 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )
 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
9.已知不等式mx+n>0的解集为x<2,则不等式(3m-n)x<2m+6n的解集是( )
| A. | x<-2 | B. | x>-2 | C. | x<14 | D. | x>14 |
10.已知?ABCD中,对角线AC、BD相交于点O,添加一个适当的条件,使?ABCD成为一个矩形.下列所加条件中,不符合要求的是( )
| A. | ∠ABC=90° | B. | AC=BD | C. | AC2=AB2+BC2 | D. | AC⊥BD |
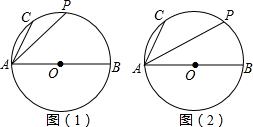
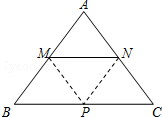 在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.
在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.
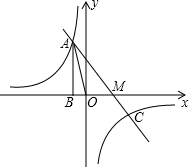 如图,已知反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,一2).
如图,已知反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,一2).