题目内容
20.已知α为锐角,当$\frac{tanα+1}{2}$=1时,求sin(α-15°)+$\sqrt{3}sin(α+15°)$的值.分析 先求出α 的值,然后代入求解.
解答 解:∵$\frac{tanα+1}{2}$=1,
∴tanα=1,
则α=45°,
sin(α-15°)+$\sqrt{3}sin(α+15°)$
=$\frac{1}{2}$+$\sqrt{3}$×$\frac{\sqrt{3}}{2}$
=2.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
相关题目
10.已知am=9,an=13,则am-n的值为( )
| A. | 4 | B. | -4 | C. | $\frac{9}{13}$ | D. | $\frac{13}{9}$ |
 如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF,若∠AOE=42°,求∠BOD的度数.
如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF,若∠AOE=42°,求∠BOD的度数.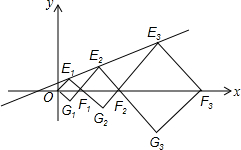 在平面直角坐标系中,点E1,E2,E3,…,和F1,F2,F3,…分别在直线y=kx+b和x轴上,四边形OE1F1G1,四边形F1E2F2G2,四边形F2E3F3G3,…都是正方形,如果E1(1,1),E2(4,2),那么线段Fn-1Fn的长是( )
在平面直角坐标系中,点E1,E2,E3,…,和F1,F2,F3,…分别在直线y=kx+b和x轴上,四边形OE1F1G1,四边形F1E2F2G2,四边形F2E3F3G3,…都是正方形,如果E1(1,1),E2(4,2),那么线段Fn-1Fn的长是( )