��Ŀ����
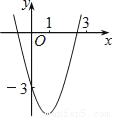
��ͼ����֪������y=x2+bx+c�����㣨0����3��������ȷ��һ��b��ֵ��ʹ����������x���һ�������ڣ�1��0���ͣ�3��0��֮�䣮��ȷ����b��ֵ��_____��
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����֪������y=x2+bx+c�����㣨0����3��������ȷ��һ��b��ֵ��ʹ����������x���һ�������ڣ�1��0���ͣ�3��0��֮�䣮��ȷ����b��ֵ��_____��
