题目内容
14.观察如图所示图形,它们是按一定规律排列的,依照此规律,第n个图形中共有( )
| A. | 3n个 | B. | (3n+1)个 | C. | (3n+2)个 | D. | (3n+3)个 |
分析 由图形可知:第1个图形五角星的个数是,1+3=4;第2个图形五角星的个数是,1+3×2=7;第3个图形五角星的个数是,1+3×3=10;第4个图形五角星的个数是,1+3×4=13;…由此得出第n个图形五角星的个数是,1+3×n=3n+1.
解答 解:观察发现,第1个图形五角星的个数是,1+3=4,
第2个图形五角星的个数是,1+3×2=7,
第3个图形五角星的个数是,1+3×3=10,
第4个图形五角星的个数是,1+3×4=13,
…
依此类推,第n个图形五角星的个数是,1+3×n=3n+1.
故选:B.
点评 本题考查了图形变化规律的问题,把五角星分成两部分进行考虑,并找出第n个图形五角星的个数的表达式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列说法中不正确的个数有( )
①1是绝对值最小的有理数;
②若a2=b2,则a3=b3;
③两个四次多项式的和一定是四次多项式;
④多项式x2-3kxy-3y2+$\frac{1}{3}$xy-8合并同类项后不含xy项,则k的值是$\frac{1}{9}$.
①1是绝对值最小的有理数;
②若a2=b2,则a3=b3;
③两个四次多项式的和一定是四次多项式;
④多项式x2-3kxy-3y2+$\frac{1}{3}$xy-8合并同类项后不含xy项,则k的值是$\frac{1}{9}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.小明的妈妈在某玩具厂工作,厂里规定每个工人每周要生产某种玩具210个,平均每天生产30个,但由于种种原因,实际每天生产量与计划量相比有出入.下表是小明妈妈某周的生产情况(超产记为正、减产记为负):
(1)根据记录的数据可知小明妈妈星期三生产玩具26个;
(2)根据记录的数据可知小明妈妈本周实际生产玩具217个;
(3)该厂实行“每日计件工资制”.每生产一个玩具可得工资5元,若超额完成任务,则超过部分每个另奖3元;少生产一个则倒扣2元,那么小明妈妈这一周的工资总额是多少元?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多?请说明理由.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减产值 | +10 | -12 | -4 | +8 | -1 | +6 | 0 |
(2)根据记录的数据可知小明妈妈本周实际生产玩具217个;
(3)该厂实行“每日计件工资制”.每生产一个玩具可得工资5元,若超额完成任务,则超过部分每个另奖3元;少生产一个则倒扣2元,那么小明妈妈这一周的工资总额是多少元?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多?请说明理由.
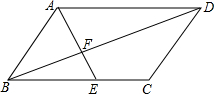 如图,在平行四边形ABCD中,BE:EC=2:1,AE与BD相交于点F,则BF:FD的值为$\frac{2}{3}$.
如图,在平行四边形ABCD中,BE:EC=2:1,AE与BD相交于点F,则BF:FD的值为$\frac{2}{3}$.
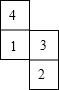 如图,这是一个由小正方块搭成的几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方体的个数,请你分别画出从正面、左面看到的形状图.
如图,这是一个由小正方块搭成的几何体的从上面看到的形状图,小正方形中的数字表示在该位置小立方体的个数,请你分别画出从正面、左面看到的形状图.