题目内容
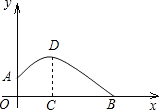 如图,一个运动员推铅球,铅球在点A处出手,出手时球离地面约1.8m.铅球落地点在B处,铅球运行中在运动员前3m处(即OC=3)达到最高点,最高点高为3.6m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
如图,一个运动员推铅球,铅球在点A处出手,出手时球离地面约1.8m.铅球落地点在B处,铅球运行中在运动员前3m处(即OC=3)达到最高点,最高点高为3.6m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?考点:二次函数的应用
专题:
分析:首先利用顶点式求出抛物线解析式,进而使y=0求出x的值,即可得出该运动员的成绩.
解答:解:由题意可得出:抛物线顶点坐标为(3,3.6),
A(0,1.8),
设抛物线解析式为:y=a(x-3)2+3.6,
将A点代入得出:1.8=a(0-3)2+3.6,
解得:a=-0.2,
故抛物线解析式为:y=-0.2(x-3)2+3.6,
当y=0时,0=-0.2(x-3)2+3.6,
解得:x1=3-3
,x2=3+3
,
故该运动员的成绩是(3+3
)m.
A(0,1.8),
设抛物线解析式为:y=a(x-3)2+3.6,
将A点代入得出:1.8=a(0-3)2+3.6,
解得:a=-0.2,
故抛物线解析式为:y=-0.2(x-3)2+3.6,
当y=0时,0=-0.2(x-3)2+3.6,
解得:x1=3-3
| 2 |
| 2 |
故该运动员的成绩是(3+3
| 2 |
点评:此题主要考查了二次函数的应用,利用顶点式求出二次函数解析式是解题关键.

练习册系列答案
相关题目
在数轴上表示不等式x-4>-1的解集,正确的是( )
A、 |
B、 |
C、 |
D、 |
下列各点在反比例函数y=
的图象上的是( )
| -6 |
| x |
| A、(3,2) | ||
| B、(-3,-2) | ||
C、(
| ||
D、(
|
已知a、b是一元二次方程x2-2x+1=0的两个实数根,则代数式(a-b)(a+b-2)+ab的值等( )
| A、2 | B、1 | C、-1 | D、3 |
 如图,在边长为1个单位的小正方形组成的网格中,△ABC的顶点都在小正方形的顶点上.
如图,在边长为1个单位的小正方形组成的网格中,△ABC的顶点都在小正方形的顶点上.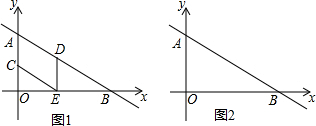 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-