题目内容
若方程（a+2）xa2-5x+3=0为一元一次方程，且点A（2a+a2，a）在第三象限，求a的值．
考点：一元一次方程的定义,点的坐标
专题：
分析：利用一元一次方程的定义求出a的值，再结合点A第三象限求出a的范围，确定a的值．
解答：解：∵方程（a+2）xa2-5x+3=0为一元一次方程，
∴当a+2≠5，a2=1，解得a=±1，当a=-2．
∵点A（2a+a2，a）在第三象限，
∴a＜0，2a+a2＜0．
∴-2＜a＜0．
∴a=-1．
∴当a+2≠5，a2=1，解得a=±1，当a=-2．
∵点A（2a+a2，a）在第三象限，
∴a＜0，2a+a2＜0．
∴-2＜a＜0．
∴a=-1．
点评：本题主要考查了一元一次方程的定义及点的坐标，解题的关键是利用定义及象限求出a的值．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
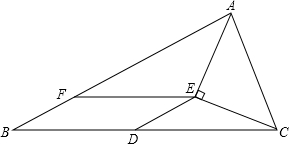如图所示，△ABC中，D是BC边上中点，AE是∠BAC的平分线，CE⊥AE，EF∥BC交AB于点F，
观察并写出该图片的规律．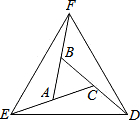
如图，△ABC中，∠BAC=∠ACB=60°，延长△ABC的各边，使BF=AC=AE=CD=AB，顺次连接D、E、F．求证：△DEF是等边三角形．
如图所示，直线L：y=mx+5m与x轴负半轴、y轴正半轴分别交于A、B两点．当OA=OB时，试确定直线L解析式．
如图，一艘帆船由于风向的原因，先向正东方航行了16千米，然后向正北方航行了20千米，这时它离出发点有多远？