题目内容
3. 我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.
我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.【提出问题】如何用表示几何图形面积的方法推证:13+23=32?
【解决问题】
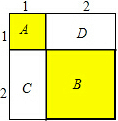
A表示1个1×1的正方形,即:1×1×1=13
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,
因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23
而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.
由此可得:13+23=32
【递进探究】请仿用上面的表示几何图形面积的方法探究:13+23+33=62.
要求:自己构造图形并写出详细的解题过程.
【推广探究】请用上面的表示几何图形面积的方法探究:13+23+33+…+n3=$\frac{{n}^{2}(n+1)^{2}}{4}$.
(参考公式:$1+2+3+…+n=\frac{(1+n)n}{2}$)
注意:只需填空并画出图形即可,不必写出解题过程.
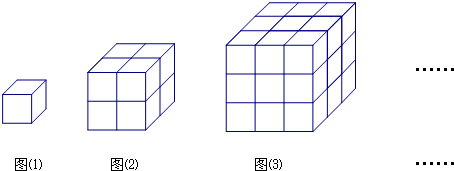
【提炼运用】如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,
如图(1)中,共有1个小立方体,其中1个看的见,0个看不见;
如图(2)中,共有8个小立方体,其中7个看的见,1个看不见;
如图(3)中,共有27个小立方体,其中19个看的见,8个看不见;
求:从第(1)个图到第(101)个图中,一切看不见的棱长为1的小立方体的总个数.
分析 【递进探究】如图,A表示一个1×1的正方形,B、C、D表示2个2×2的正方形,E、F、G表示3个3×3的正方形,而A、B、C、D、E、F、G恰好可以拼成一个边长为(1+2+3)的大正方形,根据大正方形面积的两种表示方法,可以得出13+23+33=62;
【推广探究】由上面表示几何图形的面积探究知,13+23+33+…+n3=(1+2+3+…+n)2,进一步化简即可.
解答  解:【递进探究】
解:【递进探究】
如图,A表示一个1×1的正方形,即:1×1×1=13,
B、C、D表示2个2×2的正方形,即:2×2×2=23,
E、F、G表示3个3×3的正方形,即:3×3×3=33,
而A、B、C、D、E、F、G恰好可以拼成一个大正方形,边长为:1+2+3=6,
∵SA+SB+SC+SD+SE+SF+SG=S大正方形,
∴13+23+33=62;
【推广探究】
由上面表示几何图形的面积探究知,13+23+33+…+n3=(1+2+3+…+n)2,
又∵1+2+3+…+n=$\frac{n(n+1)}{2}$,
∴13+23+33+…+n3=($\frac{n(n+1)}{2}$)2=$\frac{{n}^{2}(n+1)^{2}}{4}$.
【提炼运用】 图(1)中,共有1个小立方体,其中1个看的见,0=(1-1)3个看不见;
图(1)中,共有1个小立方体,其中1个看的见,0=(1-1)3个看不见;
如图(2)中,共有8个小立方体,其中7个看的见,1=(2-1)3个看不见;
如图(3)中,共有27个小立方体,其中19个看的见,8=(3-1)3个看不见;
…,
从第(1)个图到第(101)个图中,一切看不见的棱长为1的小立方体的总个数为:(1-1)3+(2-1)3+(3-1)3+…+(101-1)3=03+13+23+…+1003=50502=25502500.
故一切看不见的棱长为1的小立方体的总个数为25502500.
故答案为:62;$\frac{{n}^{2}(n+1)^{2}}{4}$.
点评 此题主要考查了立体图形、平方差公式的证明,注意熟练掌握通过不同的方法计算同一个图形的面积来证明一些公式的方法,利用数形结合是解题的关键.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案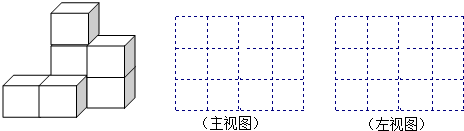
 如图所示,在正方形ABCD中,对角线AC,BD交于点O,以AC为边作等边△ACE,M为AE的中点.求证:BM⊥DM.
如图所示,在正方形ABCD中,对角线AC,BD交于点O,以AC为边作等边△ACE,M为AE的中点.求证:BM⊥DM.