题目内容
已知y-2与x成正比例,且当x=-2时,y=-4
(1)求y与x的函数表达式;
(2)作出该函数的图象;
(3)设点A(a,2)在这个函数图象上,求a;
(4)如果x的取值范围是0≤x≤5,求y的取值范围.
(1)求y与x的函数表达式;
(2)作出该函数的图象;
(3)设点A(a,2)在这个函数图象上,求a;
(4)如果x的取值范围是0≤x≤5,求y的取值范围.
考点:待定系数法求一次函数解析式,一次函数的图象,一次函数图象上点的坐标特征
专题:计算题
分析:(1)根据正比例函数的定义,设y-2=kx,即y=kx+2,然后把x=-2,y=-4代入求出k即可;
(2)利用描点法画一次函数图象;
(3)根据一次函数图象上点的坐标特征,把点A(a,2)代入(1)中的解析式即可求出a的值;
(4)分别计算出自变量为1和5所对应的函数值,然后根据一次函数的性质确定y的取值范围.
(2)利用描点法画一次函数图象;
(3)根据一次函数图象上点的坐标特征,把点A(a,2)代入(1)中的解析式即可求出a的值;
(4)分别计算出自变量为1和5所对应的函数值,然后根据一次函数的性质确定y的取值范围.
解答:解:(1)设y-2=kx,即y=kx+2,
把x=-2,y=-4代入得-2k+2=-4,解得k=3,
所以y与x的函数解析式为y=3x+2;
(2)如图:

(3)把A(a,2)代入y=3x+2得3a+2=2,解得a=0;
(4)当x=0时,y=3x+2=2;当x=5时,y=3x+2=17,
所以x的取值范围是0≤x≤5,所对应的y的取值范围为2≤y≤17.
把x=-2,y=-4代入得-2k+2=-4,解得k=3,
所以y与x的函数解析式为y=3x+2;
(2)如图:

(3)把A(a,2)代入y=3x+2得3a+2=2,解得a=0;
(4)当x=0时,y=3x+2=2;当x=5时,y=3x+2=17,
所以x的取值范围是0≤x≤5,所对应的y的取值范围为2≤y≤17.
点评:本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.也考查了一次函数图象与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
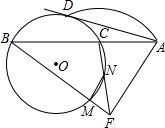 已知:如图,AD切⊙O于点D,ACB为⊙O的割线,AP=AD,BP、CP分别交⊙O于M、N.求证:
已知:如图,AD切⊙O于点D,ACB为⊙O的割线,AP=AD,BP、CP分别交⊙O于M、N.求证: