题目内容
10.解方程:(1)4x2-6x-3=0
(2)x2+9x+20=0.
分析 (1)可以根据公式法解答次方程;
(2)可以根据因式分解法解答次方程.
解答 解:(1)4x2-6x-3=0
∵a=4,b=-6,c=-3,
∴△=(-6)2-4×4×(-3)=84>0,
∴x=$\frac{6±\sqrt{84}}{2×4}=\frac{3±\sqrt{21}}{4}$,
∴x1=$\frac{3+\sqrt{21}}{4}$,x2=$\frac{3-\sqrt{21}}{4}$;
(2)x2+9x+20=0
(x+4)(x+5)=0,
∴x+4=0或x+5=0,
解得,x1=-4,x2=-5.
点评 本题考查解一元二次方程-因式分解法、公式法,解题的关键是会用因式分解法和公式法解方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.设点A(-3,a),B(b,$\frac{1}{2}$)在同一个正比例函数的图象上,则ab的值为( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | -6 | D. | $\frac{3}{2}$ |
15.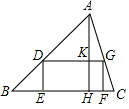 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | $\sqrt{2}$:3 |
20.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | (3a3)2=6a6 | C. | a6÷a2=a3 | D. | a2•a3=a5 |
 如图所示,已知:点D在△ABC的边AB上,连结CD,∠1=∠B,AD=4,AC=5,求AB的长.
如图所示,已知:点D在△ABC的边AB上,连结CD,∠1=∠B,AD=4,AC=5,求AB的长.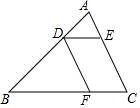 如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,则线段BF长为10cm.
如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,则线段BF长为10cm.