题目内容
 如图,在下列n×n的正方形网格中,请按图形的规律,探索以下问题:
如图,在下列n×n的正方形网格中,请按图形的规律,探索以下问题:(1)第④个图形中阴影部分小正方形的个数为
(2)是否存在阴影部分小正方形的个数是整个图形中小正方形个数的
| 7 |
| 9 |
考点:一元二次方程的应用,规律型:图形的变化类
专题:
分析:(1)观察图形,得到规律,利用规律求得第四个图形的阴影部分的小正方形的个数;
(2)根据得到的规律列出一元二次方程求解,若能求得正整数即可,否则不可.
(2)根据得到的规律列出一元二次方程求解,若能求得正整数即可,否则不可.
解答:解:(1)第一个图形阴影部分小正方形的个数为1×2+2=4个;
第二个图形阴影部分小正方形的个数为2×3+2=8个;
第三个图形阴影部分小正方形的个数为3×4+2=14个;
…
第n个图形阴影部分小正方形的个数为n(n+1)+2=n2+n+2;
当n=4时,4×(4+1)+2=22个;
(2)存在,理由是:
根据题意得n2+n+2=
(n+2)2,
整理得2n2-19n-10=0,
解得:n1=
(舍去),n2=10.
所以,第十个图形阴影部分小正方形的个数是整个图形中小正方形的个数的
.
第二个图形阴影部分小正方形的个数为2×3+2=8个;
第三个图形阴影部分小正方形的个数为3×4+2=14个;
…
第n个图形阴影部分小正方形的个数为n(n+1)+2=n2+n+2;
当n=4时,4×(4+1)+2=22个;
(2)存在,理由是:
根据题意得n2+n+2=
| 7 |
| 9 |
整理得2n2-19n-10=0,
解得:n1=
| 1 |
| 2 |
所以,第十个图形阴影部分小正方形的个数是整个图形中小正方形的个数的
| 7 |
| 9 |
点评:本题考查了图形的变化类和一元二次方程的应用,找到规律是解答本题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
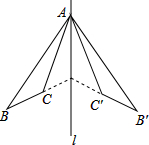 如图,△ABC和△A′B′C′关于直线对称,下列结论中:
如图,△ABC和△A′B′C′关于直线对称,下列结论中: 如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=
如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=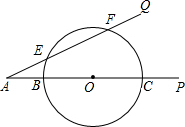 已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求: 某商店第一次用600元购进某种型号的铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.
某商店第一次用600元购进某种型号的铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支. 某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%(盈利率=
某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%(盈利率=