题目内容
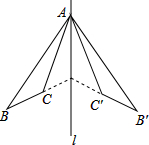 如图,△ABC和△A′B′C′关于直线对称,下列结论中:
如图,△ABC和△A′B′C′关于直线对称,下列结论中:①△ABC≌△A′B′C′;
②∠BAC′=∠B′AC;
③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
正确的有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:轴对称的性质
专题:
分析:根据关于某直线成轴对称的两个图形能够完全重合对各小题分析判断即可得解.
解答:解:∵△ABC和△A′B′C′关于直线l对称,
∴①△ABC≌△A′B′C′,正确;
②∠BAC=∠B′AC′,
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′,
即∠BAC′=∠B′AC,正确;
③l垂直平分CC′,正确;
④应为:直线BC和B′C′的交点一定在l上,故本小题错误.
综上所述,结论正确的是①②③共3个.
故选B.
∴①△ABC≌△A′B′C′,正确;
②∠BAC=∠B′AC′,
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′,
即∠BAC′=∠B′AC,正确;
③l垂直平分CC′,正确;
④应为:直线BC和B′C′的交点一定在l上,故本小题错误.
综上所述,结论正确的是①②③共3个.
故选B.
点评:本题考查轴对称的性质与运用,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
相关题目
在下列四个图案中既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列运算正确的是( )
| A、(-a3)2=a9 |
| B、a6÷a2=a3 |
| C、(a-2)2=a2-4 |
| D、2a-3a=-a |
从1999年11月1日起,全国储蓄存款征收利息税,税率是利息的20%,即储蓄利息的20%由各银行储蓄点代扣代收,小明的爸爸在2013年4月存入人民币若干元,年利率为2.25%,一年到期后将缴纳利息税72元,则小明的爸爸存入的人民币为( )
| A、1600元 |
| B、16000元 |
| C、360元 |
| D、3600元 |
方程组
的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|

 如图,四边形ABCD是平行四边形,点E、A、C、F在同一直线上,且AE=CF.求证:BE=DF.
如图,四边形ABCD是平行四边形,点E、A、C、F在同一直线上,且AE=CF.求证:BE=DF. 如图,在下列n×n的正方形网格中,请按图形的规律,探索以下问题:
如图,在下列n×n的正方形网格中,请按图形的规律,探索以下问题: