题目内容
 如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=
如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=| 3 |
| 5 |
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴正半轴方向平移使得△ABO为等腰三角形,请直接写出平移距离.
考点:作图—复杂作图,等腰三角形的判定,三角形的外接圆与外心,平移的性质,解直角三角形
专题:
分析:(1)作出BO和AB的垂直平分线,两线交点就是外接圆圆心,再画圆即可;
(2)作BH⊥OA,垂足为H首先计算出B点坐标,然后求出AB长,可得cos∠BAO;
(3)分两种情况进行计算,①当BO=AO时,②当AO=AB′时,③当AO=OB′时,因为点B是沿x轴正半轴方向平移,因此B点纵坐标不变.
(2)作BH⊥OA,垂足为H首先计算出B点坐标,然后求出AB长,可得cos∠BAO;
(3)分两种情况进行计算,①当BO=AO时,②当AO=AB′时,③当AO=OB′时,因为点B是沿x轴正半轴方向平移,因此B点纵坐标不变.
解答:解:(1)如图所示:
(2)如图,作BH⊥OA,垂足为H,
在Rt△OHB中,∵BO=10,sin∠BOA=
,
∴BH=6.
∴OH=8,
∴点B的坐标为(8,6);
∵OA=20,OH=8,
∴AH=12,
在Rt△AHB中,
∵BH=6,
∴AB=
=6
,
∴cos∠BAO=
=
;
 (3)①当BO=AO时,
(3)①当BO=AO时,
∵AO=20,
∴OH=10,
∴点B沿x轴正半轴方向平移2个单位;
②当AO=AB′时,
∵AO=20,
∴AB=20,
过B′作B′N⊥x轴,
∵点B的坐标为(8,6),
∴B′N=6,
∴AN=
=2
.
∴点B沿x轴正半轴方向平移2
+20-8=2
+12个单位;
③当AO=OB′时,
∵AO=20,
∴OB″=20,
过B″作B″P⊥x轴,
∵点B的坐标为(8,6),
∴B″P=6,
∴OP=
=2
.
∴点B沿x轴正半轴方向平移(2
-8)个单位.
(2)如图,作BH⊥OA,垂足为H,
在Rt△OHB中,∵BO=10,sin∠BOA=
| 3 |
| 5 |
∴BH=6.
∴OH=8,
∴点B的坐标为(8,6);
∵OA=20,OH=8,
∴AH=12,
在Rt△AHB中,
∵BH=6,
∴AB=
| 62+122 |
| 5 |
∴cos∠BAO=
| AH |
| BA |
2
| ||
| 5 |
 (3)①当BO=AO时,
(3)①当BO=AO时,∵AO=20,
∴OH=10,
∴点B沿x轴正半轴方向平移2个单位;
②当AO=AB′时,
∵AO=20,
∴AB=20,
过B′作B′N⊥x轴,
∵点B的坐标为(8,6),
∴B′N=6,
∴AN=
| 202-62 |
| 91 |
∴点B沿x轴正半轴方向平移2
| 91 |
| 91 |
③当AO=OB′时,
∵AO=20,
∴OB″=20,
过B″作B″P⊥x轴,
∵点B的坐标为(8,6),
∴B″P=6,
∴OP=
| 202-62 |
| 91 |
∴点B沿x轴正半轴方向平移(2
| 91 |
点评:此题主要考查了复杂作图,以及等腰三角形的判定,关键是正确画出图形,考虑分类讨论.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
下列运算正确的是( )
| A、(-a3)2=a9 |
| B、a6÷a2=a3 |
| C、(a-2)2=a2-4 |
| D、2a-3a=-a |

 如图,四边形ABCD是平行四边形,点E、A、C、F在同一直线上,且AE=CF.求证:BE=DF.
如图,四边形ABCD是平行四边形,点E、A、C、F在同一直线上,且AE=CF.求证:BE=DF. 已知:如图,在平面直角坐标系xOy中,抛物线
已知:如图,在平面直角坐标系xOy中,抛物线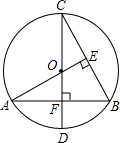 如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E,
如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为E, 如图所示,已知∠A=27°,∠CBE=90°,∠C=30°,求∠D的度数.
如图所示,已知∠A=27°,∠CBE=90°,∠C=30°,求∠D的度数. 如图,在下列n×n的正方形网格中,请按图形的规律,探索以下问题:
如图,在下列n×n的正方形网格中,请按图形的规律,探索以下问题: