题目内容
10. 如图所示,把直角三角形ABC折叠,使A与B点重合,得到折痕DE,折叠点C恰好与D点重合,求∠ABC,∠BDE的度数.
如图所示,把直角三角形ABC折叠,使A与B点重合,得到折痕DE,折叠点C恰好与D点重合,求∠ABC,∠BDE的度数.
分析 根据轴对称的性质,得DE垂直平分BC,则EA=EB,∠EBA=∠A,再结合折叠的性质,得∠ABE=∠CBE,根据直角三角形的性质计算得到答案.
解答 解:根据题意,得DE垂直平分BC,
∴∠BDE=90°,EA=EB,
∴∠EBA=∠A,
又∵∠ABE=∠CBE,∠C=90°,
∴3∠A=90°,
∠A=30°,
则∠ABC=60°.
答:∠ABC=60°,∠BDE=90°.
点评 本题考查的是折叠的性质、轴对称的性质、线段垂直平分线的性质以及直角三角形的性质,找准对应关系、灵活运用定理和性质是解题的关键.

练习册系列答案
相关题目
15.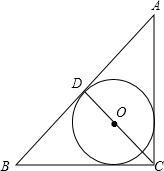 在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
 在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )| A. | CD | B. | BC | C. | AC | D. | AB |
19.减去-3x得x2-3x+4的式子为( )
| A. | x3+4 | B. | x2+3x+4 | C. | x2-6x+4 | D. | x2-6x |
20.若直线y=m(m为常数)与函数y=$\left\{\begin{array}{l}{{x}^{2}(x≤2)}\\{\frac{4}{x}(x>2)}\end{array}\right.$,则下列说法不正确的是( )
| A. | 当直线与函数图象无交点时,m<0 | |
| B. | 当直线与函数图象只有1个交点时,m≥4 | |
| C. | 当直线与函数图象只有2个交点时,2≤m≤4 | |
| D. | 当直线与函数图象有三个交点时,0<m<2 |
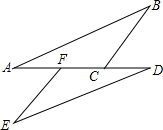 如图,在△ABC和△DEF中,AF=DC,∠A=∠D.当添加条件BC=EF时,可依据“SAS”证明△ABC≌△DEF;当添加条件∠ACB=∠DFE时,可依据”ASA”证明△ABC≌△DEF,当添加条件∠B=∠E时,可依据”AAS”证明△ABC≌△DEF.
如图,在△ABC和△DEF中,AF=DC,∠A=∠D.当添加条件BC=EF时,可依据“SAS”证明△ABC≌△DEF;当添加条件∠ACB=∠DFE时,可依据”ASA”证明△ABC≌△DEF,当添加条件∠B=∠E时,可依据”AAS”证明△ABC≌△DEF.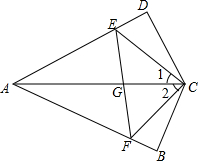 如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.
如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.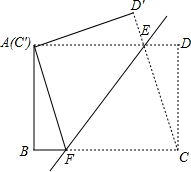 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.①AF=CD′;②△CEF是等腰三角形;③四边形AFCE为菱形;④设AE=a,ED=b,DC=c,则a、b、c三者之间的数量关系为a2=b2+c2,其中正确的结论是②③④(将所有正确结论的序号都填在横线上)
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.①AF=CD′;②△CEF是等腰三角形;③四边形AFCE为菱形;④设AE=a,ED=b,DC=c,则a、b、c三者之间的数量关系为a2=b2+c2,其中正确的结论是②③④(将所有正确结论的序号都填在横线上)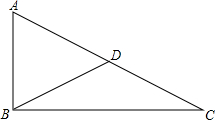 已知在△ABC中,∠A=3∠C,∠ADB=45°,D为AC的中点,求证:∠ABC=90°.
已知在△ABC中,∠A=3∠C,∠ADB=45°,D为AC的中点,求证:∠ABC=90°.