题目内容
2.如图,请同学们观察图形找出a2+b2与c2的关系:左图中,a2+b2<c2;右图中,a2+b2>c2.(填“>”“=”或“<”)通过你所学的判别直角三角形的条件,你能否大胆的猜测以下,三角形的三边满足什么条件时,它可能是钝角三角形或锐角三角形?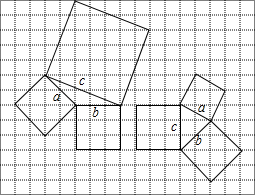
分析 左图中,由勾股定理求出a2、b2、c2,即可得出结果;
右图中,由勾股定理求出a2、b2、c2,即可得出结果;
根据题意和结果容易得出三角形的形状.
解答 解:左图中,∵a2=22+22=8,b2=32=9,
∴a2+b2=8+8=17,
∵c2=52+22=29,
∴a2+b2<c2,
故答案为:<;
右图中,∵a2=12+22=5,b2=22+22=8,
∴a2+b2=13,
∵c2=32=9,
∴a2+b2>c2,
故答案为:>;
三角形的三边a、b、c中,a和b为短边,
当a2+b2<c2时,三角形是钝角三角形;
当a2+b2>c2时,三角形是锐角三角形.
点评 本题考查了勾股定理、三角形形状的判定方法;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
19.减去-3x得x2-3x+4的式子为( )
| A. | x3+4 | B. | x2+3x+4 | C. | x2-6x+4 | D. | x2-6x |
 若将三个数-$\sqrt{3}$,$\sqrt{7}$,$\root{3}{11}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{7}$,$\root{3}{11}$.
若将三个数-$\sqrt{3}$,$\sqrt{7}$,$\root{3}{11}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{7}$,$\root{3}{11}$.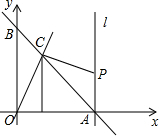 如图,直线y=-x+6与坐标轴交于A、B两点,与直线y=2x交于C点,直线是过A点且垂直x轴的直线,点P是直线l上的一动点.
如图,直线y=-x+6与坐标轴交于A、B两点,与直线y=2x交于C点,直线是过A点且垂直x轴的直线,点P是直线l上的一动点. 如图,在△ABC中,若D、E分别是AB、AC上的点,且DE∥BC,AD=1,BD=2,则DE:BC=1:3.
如图,在△ABC中,若D、E分别是AB、AC上的点,且DE∥BC,AD=1,BD=2,则DE:BC=1:3.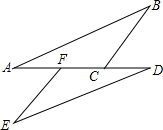 如图,在△ABC和△DEF中,AF=DC,∠A=∠D.当添加条件BC=EF时,可依据“SAS”证明△ABC≌△DEF;当添加条件∠ACB=∠DFE时,可依据”ASA”证明△ABC≌△DEF,当添加条件∠B=∠E时,可依据”AAS”证明△ABC≌△DEF.
如图,在△ABC和△DEF中,AF=DC,∠A=∠D.当添加条件BC=EF时,可依据“SAS”证明△ABC≌△DEF;当添加条件∠ACB=∠DFE时,可依据”ASA”证明△ABC≌△DEF,当添加条件∠B=∠E时,可依据”AAS”证明△ABC≌△DEF.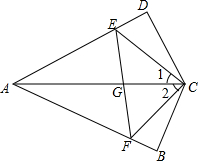 如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.
如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.