��Ŀ����
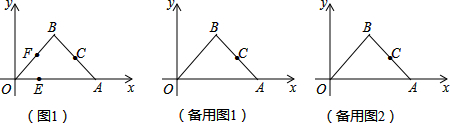
11����֪����ͼ1����ƽ��ֱ�������У�A��12��0����B��6��6������CΪ�߶�AB���е㣬��D��ԭ��O���ڵ�C�Գƣ���1������ֱ�ߺ�Բ����ͼ1��������D��λ�ã�������ͼ�ۼ������ж��ı���OBDA����״����˵�����ɣ�
��2����ͼ1�У�����E�ӵ�O��������ÿ��1����λ���ٶ����߶�OA�˶��������Aʱֹͣ��ͬʱ������F�ӵ�O��������ÿ��a����λ���ٶ���OB��BD��DA�˶��������Aʱֹͣ�����˶���ʱ��Ϊt���룩��
�ٵ�t=4ʱ��ֱ��EFǡ��ƽ���ı���OBDA���������a��ֵ��
�ڵ�t=5ʱ��CE=CF����ֱ��д��a��ֵ��
���� ��1��������OC����ȡCD=OC��Ȼ���ɶԽ�����ƽ�ֵ��ı�����ƽ���ı��ν��пɵõ��ı��ε���״��
��2������ֱ��EFǡ��ƽ���ı���OBDA�������ֱ֪��EF�ع�C����������֤����OEC�ա�DFC���Ӷ������DF�ij��ȣ����ǵõ�BF=8��Ȼ�����������ľ��빫ʽ���OB�ij����Ӷ������a��ֵ��
������õ�E�����꣬Ȼ�����EC�ij����Ӷ��õ�CF1�ij���Ȼ�����ݹ��ɶ������涨��֤����OBA=90�㣬�ڡ�BCF1�У����ݹ��ɶ��������BF1�ij����Ӷ������a��ֵ�����F2�����꣨b��6������CE=CF�г�����b�ķ��̿���õ�F2�����꣬�Ӷ������a��ֵ����Rt��CAF3�У�ȡ��AF3�ij����Ӷ���õ�F�˶���·�̣����ǿ����a��ֵ��
��� �⣺��1����ͼ��ʾ��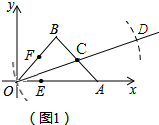
�ı���OBDA��ƽ���ı��Σ�
�������£��ߵ�CΪ�߶�AB���е㣬
��CB=CA��
�ߵ�D��ԭ��O���ڵ�C�Գƣ�
��CO=CD��
���ı���OBDA��ƽ���ı��Σ�
��2������ͼ2��ʾ��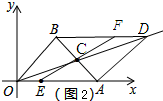
��ֱ��EFǡ��ƽ���ı���OBDA�������
��ֱ��EF�ع�C��9��3����
��t=4��
��OE=4��
��BD��OA��
���COE=��CDF��
���ڡ�OEC�͡�DFC��$\left\{\begin{array}{l}{��COE=��CDF}\\{OC=OD}\\{��OCE=��DCF}\end{array}\right.$��
���OEC�ա�DFC��
��DF=OE=4��
��BF=12-4=8��
�������ľ��빫ʽ��֪OB=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$��
��4a=6$\sqrt{2}$+8��
��a=2+$\frac{3}{2}$$\sqrt{2}$��
����ͼ3��ʾ��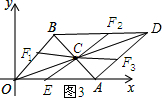
�ߵ�t=5ʱ��OE=5��
���E�����꣨5��0����
�������ľ��빫ʽ��֪EC=$\sqrt{��9-5��^{2}+��3-0��^{2}}$=5��
��CE=CF��
��CF=5��
�������ľ��빫ʽ��֪OB=BA=6$\sqrt{2}$��
�֡�OA=12��
���OBAΪֱ�������Σ�
���OBA=90�㣮
����ֱ�ǡ�F1BC�У�CF1=5��BC=3$\sqrt{2}$��
��BF1=$\sqrt{7}$��
��OF1=6$\sqrt{2}$-$\sqrt{7}$��
��a=$\frac{6\sqrt{2}-\sqrt{7}}{5}$��
����F2������Ϊ��b��6�����������ľ��빫ʽ��֪$\sqrt{��9-b��^{2}+��6-3��^{2}}$=5��
��ã�b=5����ȥ����b=13��
��BF2=13-6=7��
��OB+BF2=6$\sqrt{2}$+7��
��a=$\frac{6\sqrt{2}+7}{5}$��
�ۡ�BO��AD��
���BAD=��OBA=90�㣮
��AF3=$\sqrt{C{{F}_{3}}^{2}-A{C}^{2}}$=$\sqrt{7}$��
��DF3=6$\sqrt{2}$-$\sqrt{7}$��
��OB+BD+DF3=6$\sqrt{2}$+12+6$\sqrt{2}$-$\sqrt{7}$=12$\sqrt{2}$-$\sqrt{7}$+12��
��a=$\frac{12\sqrt{2}-\sqrt{7}+12}{5}$��
��������a��ֵΪ$\frac{6\sqrt{2}-\sqrt{7}}{5}$��$\frac{6\sqrt{2}+7}{5}$��$\frac{12\sqrt{2}-\sqrt{7}+12}{5}$��
���� ������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ����ƽ���ı��ε��ж���ȫ�������ε����ʺ��ж������ɶ������ɶ������涨����Ӧ�ã������ľ��빫ʽ���F1B��F2D��F3A�ij����ǽ���Ĺؼ���

| A�� | 100��1+x�� | B�� | 100��1+x��2 | C�� | 100��1+x2�� | D�� | 100��1+2x�� |
 ��ͼ����ƽ��ֱ������ϵxOy�У�����ABCD�Ķ���A��3��0����B��0��4������ͼ�����C�ķ�������������ʽΪ��������
��ͼ����ƽ��ֱ������ϵxOy�У�����ABCD�Ķ���A��3��0����B��0��4������ͼ�����C�ķ�������������ʽΪ��������| A�� | $y=\frac{20}{x}$ | B�� | $y=-\frac{20}{x}$ | C�� | $y=\frac{12}{x}$ | D�� | $y=-\frac{12}{x}$ |
 ��һ����ֱ�Ĺ�·����A��B��C���أ�C��λ��A��B����֮�䣬�ף��������ֱ��A��B���س�������������·������ʻ��C��ֹͣ���Ӽ׳��������׳�����C�صĹ��̣��ס�������������C�صľ���y��km����׳���ʻʱ��t��h��֮��ĺ�����ϵ��ͼ��ʾ�����׳�����$\frac{3}{2}$hʱ���������350km��
��һ����ֱ�Ĺ�·����A��B��C���أ�C��λ��A��B����֮�䣬�ף��������ֱ��A��B���س�������������·������ʻ��C��ֹͣ���Ӽ׳��������׳�����C�صĹ��̣��ס�������������C�صľ���y��km����׳���ʻʱ��t��h��֮��ĺ�����ϵ��ͼ��ʾ�����׳�����$\frac{3}{2}$hʱ���������350km��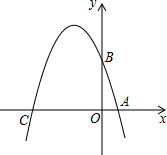 ��֪��ͼ����ƽ��ֱ������ϵxOy�У���A��B��C�ֱ�Ϊ�������ϵ������㣬��OA=1��OB=3��OC=4��
��֪��ͼ����ƽ��ֱ������ϵxOy�У���A��B��C�ֱ�Ϊ�������ϵ������㣬��OA=1��OB=3��OC=4��