题目内容
13. 点P为反比例函数y=$\frac{{k}_{1}}{x}$上一点,向x,y轴上作垂线,交反比例函数y=$\frac{{k}_{2}}{x}$上于点A,B,交x轴于点D,交y轴于点C,则
点P为反比例函数y=$\frac{{k}_{1}}{x}$上一点,向x,y轴上作垂线,交反比例函数y=$\frac{{k}_{2}}{x}$上于点A,B,交x轴于点D,交y轴于点C,则(1)S△OAC=S△OBD;
(2)A为PC中点时,S△OCA=S△AOP=S△POB=S△BOD;
(3)A为PC中点时,B为PD中点;
(4)$\frac{AC}{PC}$=$\frac{1}{n}$时,$\frac{BD}{PD}$=$\frac{1}{n}$;
(5)S四边形AOBP=|k1-k2|为定值.
分析 (1)根据反比例函数的性质直接得出结论;
(2)利用三角形的面积公式以及等底同高的两三角形面积相等即可;
(3)同(2)的方法即可;
(4)利用同高的两三角形面积的比是底的比即可;
(5)利用图形的面积差即可,
解答 解:(1)如图,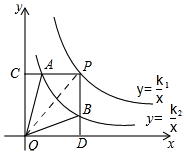
连接OP,
∵点A在反比例函数y=$\frac{{k}_{2}}{x}$上,
∴S△AOC=$\frac{1}{2}$|k2|
∵点B在反比例函数y=$\frac{{k}_{2}}{x}$上,
∴S△BOD=$\frac{1}{2}$|k2|,
∴S△AOC=S△BOD,
(2)∵A为PC中点,
∴AC=PA,
∵PC⊥y轴,
∴S△AOC=$\frac{1}{2}$AC×OC,S△AOP=$\frac{1}{2}$AP×OC,
∴S△AOC=S△AOP,
由(1)知,S△AOC=S△BOD,
∴S△AOC=S△AOP=S△BOD,
∵S△POC=S△POD,
∴S△AOP=S△POB,
∴S△OCA=S△AOP=S△POB=S△BOD,
(3)由(2)知S△POB=S△BOD
∵S△POB=$\frac{1}{2}$PB×OD,S△DOB=$\frac{1}{2}$DB×OD,
∴PD=DB,
∴点B是PD中点;
(4)由(2)知,S△AOC=$\frac{1}{2}$AC×OC,S△AOP=$\frac{1}{2}$AP×OC,
∵$\frac{AC}{PC}$=$\frac{1}{n}$,
∴$\frac{{S}_{△AOC}}{{S}_{△AOP}}=\frac{1}{n}$,
∵S△BOD=S△AOC,S△POD=S△POC,
∴S△BOP=S△AOP
∴$\frac{{S}_{△BOD}}{{S}_{△BOP}}=\frac{1}{n}$,
∵S△POB=$\frac{1}{2}$PB×OD,S△DOB=$\frac{1}{2}$DB×OD,
∴$\frac{BD}{PD}$=$\frac{1}{n}$;
(5)点P在为反比例函数y=$\frac{{k}_{1}}{x}$上,且PC⊥y轴,PD⊥x轴,
∴S四边形OCPD=k1,
∵反比例函数y=$\frac{{k}_{2}}{x}$上于点A,B,
∴S△AOC+S△BOD=k2,
∴S四边形AOBP=S四边形OCPD-(|S△AOC+S△BOD)=|k1-k2|.
点评 此题是反比例函数综合题,主要考查了反比例函数的性质,三角形的面积公式,同底等高的三角形的面积关系,同高的两三角形的面积比等于底的比,解本题的关键是利用反比例函数的性质.

 阅读快车系列答案
阅读快车系列答案 如图正方形网格中,sin∠ABC的值为( )
如图正方形网格中,sin∠ABC的值为( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
| A. | a | B. | $\frac{1}{a}$ | C. | $\sqrt{a}$ | D. | a2 |
 如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示2015的点与圆周上表示数字哪个点重合?( )
如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示2015的点与圆周上表示数字哪个点重合?( )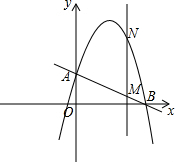 如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.
如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A,B两点,抛物线y=-x2+bx+c过A,B两点.