如图正方形网格中.sin∠ABC的值为( )A．1B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．$\sqrt{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

3．

如图正方形网格中，sin∠ABC的值为（　　）

A．

B．

$\frac{\sqrt{2}}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

$\sqrt{2}$

分析先根据正方形网格的特点得出∠ACB=90°，求出AC，AB即可；

解答解：连接BC，如图，
根据网格得出AC=$\sqrt{5}$，AB=$\sqrt{10}$，BC=$\sqrt{5}$，
∴AC²+BC²=AB²，
∴∠ACB=90°，
在Rt△ABC中，sin∠ABC=$\frac{AC}{AB}$=$\frac{\sqrt{2}}{2}$．
故选B

点评本题是特殊角的三角函数，比较简单，主要考查的是锐角三角函数的定义及正方形网格的特点．

练习册系列答案

相关题目

17．

如图，在△ABC中，∠C=65°，∠ADB=85°，AD是△ABC的角平分线，求∠B的度数．

14．在△ABC中，边AB、AC的垂直平分线交于点P，
求证：点P在△ABC的垂直平分线上．

11．已知，△ABC是边长3cm的等边三角形．动点P以1cm/s的速度从点A出发，沿线段AB向点B运动．
（1）如图1，设点P的运动时间为t（s），那么t为何值时，△PBC是直角三角形；
（2）若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D．如果动点P、Q都以1cm/s的速度同时出发．
①如图2，设运动时间为t（s），那么t为何值时，△DCQ是等腰三角形？
②如图3，连接PC，请你猜想：在点P、Q的运动过程中，△PCD和△QCD的面积有什么关系？并说明理由．

18．已知分式方程$\frac{x}{x-2}$-$\frac{1}{{x}^{2}-4}$=1，去分母后得（　　）

8．用配方法解3x²-6x=6配方得（　　）

15．把1米的线段进行黄金分割，则分成的较短的线段长为（　　）

A．

$\frac{3-\sqrt{5}}{2}$

B．

$\frac{\sqrt{5}-1}{2}$

C．

$\frac{1+\sqrt{5}}{2}$

D．

$\frac{3+\sqrt{5}}{2}$

12．

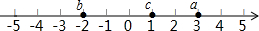如图，数轴上有3个点，它们所表示的数分别用a，b，c．
（1）在数轴上标出a，b，c的相反数-a，-b，-c；
（2）把a，b，c和它们的相反数用“＜”连接起来；
（3）如果将表示数a的点向左移动3个单位长度，同时将表示数b的点向右移动5个单位长度，表示数c的点保持在原来的位置，则移动后的a，b，c三个数的大小关系如何？

13．

点P为反比例函数y=$\frac{{k}_{1}}{x}$上一点，向x，y轴上作垂线，交反比例函数y=$\frac{{k}_{2}}{x}$上于点A，B，交x轴于点D，交y轴于点C，则
（1）S_△OAC=S_△OBD；
（2）A为PC中点时，S_△OCA=S_△AOP=S_△POB=S_△BOD；
（3）A为PC中点时，B为PD中点；
（4）$\frac{AC}{PC}$=$\frac{1}{n}$时，$\frac{BD}{PD}$=$\frac{1}{n}$；
（5）S_{四边形AOBP}=|k₁-k₂|为定值．

试题分类