题目内容
 如图,两个圆都以O为圆心,则下面等式一定成立的是
如图,两个圆都以O为圆心,则下面等式一定成立的是
- A.AB=CD
- B.AB=BC
- C.BC=CD
- D.AD=2BC
A
分析:过圆心O作弦AD的垂线,由垂径定理得到E为AD的中点,E为BC的中点,利用等式的性质即可得到AB=CD.
解答: 解:过O作OE⊥AD,
解:过O作OE⊥AD,
由垂径定理得到:E为BC中点,E为AD中点,
∴AE=DE,BE=CE,
则AE-BE=DE-CE,即AB=CD.
故选A
点评:此题考查了垂径定理,以及等式的性质,熟练掌握垂径定理是解本题的关键.
分析:过圆心O作弦AD的垂线,由垂径定理得到E为AD的中点,E为BC的中点,利用等式的性质即可得到AB=CD.
解答:
 解:过O作OE⊥AD,
解:过O作OE⊥AD,由垂径定理得到:E为BC中点,E为AD中点,
∴AE=DE,BE=CE,
则AE-BE=DE-CE,即AB=CD.
故选A
点评:此题考查了垂径定理,以及等式的性质,熟练掌握垂径定理是解本题的关键.

练习册系列答案
相关题目
 如图,两个圆都以点O为圆心,且CD=3cm,
如图,两个圆都以点O为圆心,且CD=3cm,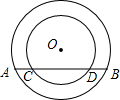 (2013•武汉模拟)如图,两个圆都以点O为圆心.求证:AC=BD.
(2013•武汉模拟)如图,两个圆都以点O为圆心.求证:AC=BD. 如图,两个圆都以O为圆心,则下面等式一定成立的是( )
如图,两个圆都以O为圆心,则下面等式一定成立的是( ) 为圆心,大圆的弦
为圆心,大圆的弦 交小圆于
交小圆于 、
、 两点.
两点. =
= .
.