题目内容
 如图,两个圆都以点O为圆心,且CD=3cm,
如图,两个圆都以点O为圆心,且CD=3cm,(1)线段AB的长;
(2)若BC=2,且小圆半径为
| 2 |
分析:(1)过点O作OE⊥BC于点E,由于BC、AD分别为两个圆的弦,故可知AE=DE,BE=CE,即可求出AB的长,
(2)连接OC,OD,OE⊥BC,BC=2,则可以求出CE=1,利用勾股定理求出EO,再次利用勾股定理求出OD的长.
(2)连接OC,OD,OE⊥BC,BC=2,则可以求出CE=1,利用勾股定理求出EO,再次利用勾股定理求出OD的长.
解答: 解:(1)过点O作OE⊥BC于点E,
解:(1)过点O作OE⊥BC于点E,
∵BC、AD分别为两个圆的弦,
∴AE=DE,BE=CE,
∴AB=CD=3cm,
(2)连接OC,OD,则OC=
∵OE⊥BC,BC=2
∴EC=1
由勾股定理得:EO=1
∴ED=4,
由勾股定理得:OD=
,即大圆半径为
cm.
 解:(1)过点O作OE⊥BC于点E,
解:(1)过点O作OE⊥BC于点E,∵BC、AD分别为两个圆的弦,
∴AE=DE,BE=CE,
∴AB=CD=3cm,
(2)连接OC,OD,则OC=
| 2 |
∵OE⊥BC,BC=2
∴EC=1
由勾股定理得:EO=1
∴ED=4,
由勾股定理得:OD=
| 17 |
| 17 |
点评:本题主要考查垂径定理和勾股定理的知识点,解答本题的关键是熟练掌握勾股定理和垂径定理的应用,本题难度一般.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 18、如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一直线上.你认为AC与BD的大小有何关系?说明理由.
18、如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一直线上.你认为AC与BD的大小有何关系?说明理由. (2012•南漳县模拟)如图,两个圆都以点O为圆心,大圆的弦DE交小圆于B,C两点,A为小圆上一点,且
(2012•南漳县模拟)如图,两个圆都以点O为圆心,大圆的弦DE交小圆于B,C两点,A为小圆上一点,且
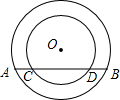 (2013•武汉模拟)如图,两个圆都以点O为圆心.求证:AC=BD.
(2013•武汉模拟)如图,两个圆都以点O为圆心.求证:AC=BD. 为圆心,大圆的弦
为圆心,大圆的弦 交小圆于
交小圆于 、
、 两点.
两点. =
= .
.